12．设i为虚数单位，则$\frac{3-i}{i}$=（　　）

A．

-1-3i

B．

1-3i

C．

-1+3i

D．

1+3i

11．已知椭圆C的中心在原点O，焦点在x轴上，离心率为$\frac{1}{2}$，右焦点到右顶点的距离为1．
（1）求椭圆C的标准方程；
（2）是否存在与椭圆C交于A、B两点的直线l：y=kx+m（k∈R），使得以AB为直径的圆过原点？若存在，求出实数m的取值范围，若不存在，请说明理由．

10．某校在一次高三年级“诊断性”测试后，对该年级的500名考生的成绩进行统计分析，成绩的频率分布表及频率分布直方图如图所示，规定成绩不小于130分为优秀．
（1）若用分层抽样的方法从这500人中抽取5人的成绩进行分析，求其中成绩为优秀的学生人数；
（2）在（1）中抽取的5名学生中，要随机抽取2名学生参加分析座谈会，求恰有1人成绩为优秀的概率．

区间	人数
[115，120）	25
[120，125）	a
[125，130）	175
[130，135）	150
[135，140）	b

9．已知$\overrightarrow{OA}$=（cos²x，-1），$\overrightarrow{OB}$=（1，sin²x+$\sqrt{3}$sin2x）（x∈R），若f（x）=$\overrightarrow{OA}$•$\overrightarrow{OB}$，则函数f（x）的最小正周期（　　）

A．

$\frac{π}{2}$

B．

π

C．

2π

D．

4π

8．某种多面体玩具共有12个面，在其十二个面上分别标有数字1，2，3，…，12．若该玩具质地均匀，则抛掷该玩具后，任何一个数字所在的面朝上的概率均相等．抛掷该玩具一次，记事件A=“向上的面标记的数字是完全平方数（记能写出整数的平方形式的数，如9=3²，9是完全平方数）”
（1）甲、乙二人利用该玩具进行游戏，并规定：
①甲抛掷一次，若事件A发生，则向上一面的点数的6倍为甲的得分；若事件A不发生，则甲得0分；②乙抛掷一次，将向上的一面对应的数字作为乙的得分；
（ⅰ） 甲、乙二人各抛掷该玩具一次，求二人得分的期望；
（ⅱ）甲、乙二人各抛掷该玩具一次，求甲的得分不低于乙的概率；
（2）抛掷该玩具一次，记事件B=“向上一面的点数不超过k（1≤k≤12）”，若事件A与B相互独立，试求出所有的整数k．

7．已知函数$f（x）=xcosx-\frac{a}{x}sinx-sinx，x∈（{-kπ，0}）∪（{0，kπ}）$（其中k为正整数，a∈R，a≠0），则f（x）的零点个数为（　　）

A．

2k-2

B．

2k

C．

2k-1

D．

与a有关

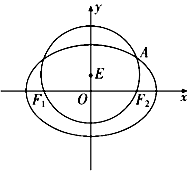6．如图，已知圆E：${x^2}+{（{y-\frac{1}{2}}）^2}=\frac{9}{4}$经过椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左右焦点F₁，F₂，与椭圆C在第一象限的交点为A，且F₁，E，A三点共线．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设与直线OA（O为原点）平行的直线l交椭圆C于M，N两点．当△AMN的面积取到最大值时，求直线l的方程．

5．2015年12月，京津冀等地数城市指数“爆表”，北方此轮污染为2015年以来最严重的污染过程．为了探究车流量与PM2.5的浓度是否相关，现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表：

时间	星期一	星期二	星期三	星期四	星期五	星期六	星期七
车流量x（万辆）	1	2	3	4	5	6	7
PM2.5的浓度y（微克/立方米）	28	30	35	41	49	56	62

（Ⅰ）由散点图知y与x具有线性相关关系，求y关于x的线性回归方程；
（Ⅱ）（ⅰ）利用（Ⅰ）所求的回归方程，预测该市车流量为8万辆时PM2.5的浓度；
（ⅱ）规定：当一天内PM2.5的浓度平均值在（0，50]内，空气质量等级为优；当一天内PM2.5的浓度平均值在（50，100]内，空气质量等级为良．为使该市某日空气质量为优或者为良，则应控制当天车流量在多少万辆以内？（结果以万辆为单位，保留整数．）
参考公式：回归直线的方程是$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其中$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．

4．已知$α∈（{0，\frac{π}{4}}）$，$sin（{α+\frac{π}{4}}）=\frac{4}{5}$，则tanα=$\frac{1}{7}$．

3．若曲线y=lnx+ax²-2x（a为常数）不存在斜率为负数的切线，则实数a的取值范围是[$\frac{1}{2}$，+∞）．