练习册

  • 练习册
  • 试题
    相关习题
     0  237524  237532  237538  237542  237548  237550  237554  237560  237562  237568  237574  237578  237580  237584  237590  237592  237598  237602  237604  237608  237610  237614  237616  237618  237619  237620  237622  237623  237624  237626  237628  237632  237634  237638  237640  237644  237650  237652  237658  237662  237664  237668  237674  237680  237682  237688  237692  237694  237700  237704  237710  237718  266669 

    科目： 来源： 题型：填空题

    12．已知圆M与y轴相切，圆心在直线y=$\frac{1}{2}$x上，并且在x轴上截得的弦长为2$\sqrt{3}$．则圆M的标准方程为（x-2）2+（y-1）2=4或（x+2）2+（y+1）2=4．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．已知点A（a，0），点P是双曲线C：$\frac{{x}^{2}}{4}$-y2=1右支上任意一点，若|PA|的最小值为3，则满足条件的A点个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．已知函数f（x）=ax+b，若0＜f（1）＜2，-1＜f（-1）＜1，则2a-b的取值范围是（　　）
    A．（-$\frac{3}{2}$，$\frac{5}{2}$）B．（$\frac{3}{2}$，$\frac{5}{2}$）C．（-$\frac{5}{2}$，$\frac{7}{2}$）D．（$\frac{5}{2}$，$\frac{7}{2}$）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    9．《九章算术》是研究比率方面应用十分丰富，其中有著名的“米谷粒分”问题：粮仓收粮，粮农运来米1520石，为验其米内夹谷，随机取米一把，数得144粒内夹谷18粒，则这批米内夹谷约为（　　）
    A．170石B．180石C．190石D．200石

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{a}$=1，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    7．已知a，b∈R，i为虚数单位，当a+bi=i（2-i）时，则$\frac{b+ai}{a-bi}$=（　　）
    A．iB．-iC．1+iD．1-i

    查看答案和解析>>

    科目： 来源： 题型：选择题

    6．已知全集U={x∈N|x≤5}，若A={x∈N|2x-5＜0}，则∁UA=（　　）
    A．{3，4}B．{3，4，5}C．{2，3，4，5}D．{4，5}

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．已知椭圆C；$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞c）的左、右焦点分别为F1（-c，0）、F2（c，0），过原点O的直线（与x轴不重合）与椭圆C相交于D、Q两点，且|DF1|+|QF1|=4，P为椭圆C上的动点，△PF1F2的面积的最大值为$\sqrt{3}$．
    （1）求椭圆C的离心率；
    （2）若A、B是椭圆C上关于x轴对称的任意两点，设点N（-4，0），连接NA与椭圆C相交于点E，直线BE与x轴相交于点M，试求$\frac{N{F}_{2}}{M{F}_{2}}$的值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

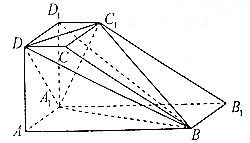    4．如图，直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形，其中AB⊥AD，AB=2AD=2AA1=4，CD=1．
    （Ⅰ）证明：BD1⊥平面A1C1D；
    （Ⅱ）求BD1与平面A1BC1所成角的正弦值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

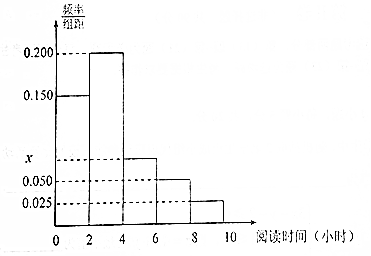    3．某学校为了了解本校高一学生每周课外阅读时间（单位：小时）的情况，按10%的比例对该校高一600名学生进行抽样统计，将样本数据分为5组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10），并将所得数据绘制成如图所示的频率分布直方图：
    （Ⅰ）求图中的x的值；
    （Ⅱ）估计该校高一学生每周课外阅读的平均时间；
    （Ⅲ）为了进一步提高本校高一学生对课外阅读的兴趣，学校准备选拔2名学生参加全市阅读知识竞赛，现决定先在第三组、第四组、第五组中用分层抽样的放法，共随机抽取6名学生，再从这6名学生中随机抽取2名学生代表学校参加全市竞赛，在此条件下，求第三组学生被抽取的人数X的数学期望．

    查看答案和解析>>

    同步练习册答案