6．设等差数列{a_n}的前n项和为S_n，若S₉=54，则a₂+a₄+a₉=（　　）

A．

9

B．

15

C．

18

D．

36

5．设|a|＜1，函数f（x）=ax²+x-a（-1≤x≤1），证明：|f（x）|≤$\frac{5}{4}$．

4．在抛物线y²=4a（x+a）（a＞0），设有过原点O作一直线分别交抛物线于A、B两点，如图所示，试求|OA|•|OB|的最小值．

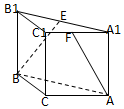3．如图，ABC-A₁B₁C₁是直三棱柱，∠BCA=90°，点E、F分别是A₁B₁、A₁C₁的中点，若BC=CA=AA₁，则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$．

2．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率是$\frac{\sqrt{2}}{2}$，F₁、F₂是椭圆的左、右焦点，点A为椭圆的右顶点，点B为椭圆的上顶点，且S${\;}_{△AB{F}_{1}}$=$\frac{\sqrt{2}+1}{2}$．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若直线l过右焦点F₂且交椭圆E于P、Q两点，点M是直线x=2上的任意一点，直线MP、MF₂、MQ的斜率分别为k₁、k₂、k₃，问是否存在常数λ，使得k₁+k₃=λk₂成立？若存在，求出λ的值；若不存在，请说明理由．

1．为响应阳光体育运动的号召，某县中学生足球活动正如火如荼的开展，该县为了解本县中学生的足球运动状况，根据性别采取分层抽样的方法从全县24000名中学生（其中男生14000人，女生10000人）中抽取120名，统计他们平均每天足球运动的时间，如表：（平均每天足球运动的时间单位为小时，该县中学生平均每天足球运动的时间范围是[0，3]）
男生平均每天足球运动的时间分布情况：

平均每天足球运动的时间	[0，0.5）	[0.5，1）	[1，1.5）	[1.5，2）	[2，2.5）	[2.5，3]
人数	2	3	28	22	10	x

女生平均每天足球运动的时间分布情况：

平均每天足球运动的时间	[0，0.5）	[0.5，1）	[1，1.5）	[1.5，2）	[2，2.5）	[2.5，3]
人数	5	12	18	10	3	y

（Ⅰ）请根据样本估算该校男生平均每天足球运动的时间（结果精确到0.1）；
（Ⅱ）若称平均每天足球运动的时间不少于2小时的学生为“足球健将”．低于2小时的学生为“非足球健将”．
①请根据上述表格中的统计数据填写下面2×2列联表，并通过计算判断，能否有90%的把握认为是否为“足球健将”与性别有关？

	足球健将	非足球健将	总　　计
男　　生
女　　生
总　　计

②若在足球活动时间不足1小时的男生中抽取2名代表了解情况，求这2名代表都是足球运动时间不足半小时的概率．
参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

P（K2＞k0）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010
k0	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635

20．执行如图所示的程序框图，则输出S的值为（　　）

A．

16

B．

32

C．

64

D．

1024

19．对实数a与b，定义新运算“?”：a?b=$\left\{\begin{array}{l}{a，a-b≤1}\\{b，a-b＞1}\end{array}\right.$．设函数f（x）=（x²-2）?（x-x²），x∈R．若函数y=f（x）-c的零点恰有两个，则实数c的取值范围是（　　）

A．

（-∞，-2]∪（-1，$\frac{3}{2}$）

B．

（-∞，-2]∪（-1，-$\frac{3}{4}$）

C．

（-∞，$\frac{1}{4}$）∪（$\frac{1}{4}$，+∞）

D．

（-1，-$\frac{3}{4}$）∪[$\frac{1}{4}$，+∞）

18．已知实数2，m，$\frac{9}{2}$依次构成一个等比数列，则圆锥曲线x²+$\frac{{y}^{2}}{m}$=1的离心率为（　　）

A．

$\frac{\sqrt{6}}{3}$

B．

$\frac{2\sqrt{3}}{3}$

C．

$\frac{\sqrt{6}}{3}$或2

D．

$\frac{2\sqrt{3}}{3}$或2

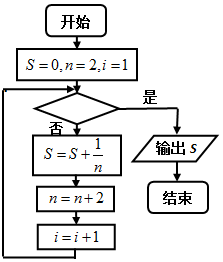17．如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图，其中判断框内应填入的条件是（　　）

A．

i＞8

B．

i＞9

C．

i＞10

D．

i＞11