2．已知集合A={x|log${\;}_{\frac{1}{2}}$（x+1）≥-2}，B={x|$\frac{x+2}{1-x}$≥2}，则 A∩B=（　　）

A．

（-1，1）

B．

[0，1）

C．

[0，3]

D．

∅

1．过点P（1，0）与抛物线y=x²有且只有一个公共点的直线共有（　　）

A．

4条

B．

3条

C．

2条

D．

1条

20．函数y=2^x+1的反函数是（　　）

	A．	y=logx2+1，x＞0且x≠1		B．	y=log2x+1，x＞0
	C．	y=log2x-1，x＞0		D．	y=log2（x-1），x＞1

19．已知数列{a_n}中，a₁=2，na_n+1=2（n+1）a_n，则a₅=（　　）

A．

320

B．

160

C．

80

D．

40

18．若圆C：x²+y²=4上的点到直线l：y=x+a的最小距离为2，则a=（　　）

A．

$2\sqrt{2}$

B．

$4\sqrt{2}$

C．

$±2\sqrt{2}$

D．

$±4\sqrt{2}$

17．已知等差数列{a_n}的首项a₁=1，公差d＞0，且第二项，第五项，第十四项分别是等比数列{b_n}的第二项，第三项，第四项．
（1）求数列{a_n}与{b_n}的通项公式．
（2）设数列{c_n}对任意正整数n，均有$\frac{c_1}{b_1}+\frac{c_2}{b_2}+\frac{c_3}{b_3}+…+\frac{c_n}{b_n}={a_{n+1}}$，求c₁+c₂+c₃+…+c₂₀₀₄的值．

16．已知双曲线的焦点分别为（0，-2）、（0，2），且经过点P（-3，2），则双曲线的标准方程是（　　）

A．

$\frac{x^2}{3}-{y^2}$=1

B．

$\frac{y^2}{3}-{x^2}$=1

C．

y2-$\frac{x^2}{3}$=1

D．

$\frac{x^2}{2}-\frac{y^2}{2}$=1

15．已知圆C：（x-1）²+（y-2）²=25及直线l：（2m+1）x+（m+1）y=7m+4（m∈R），则直线l过的定点及直线与圆相交得的最短弦长分别为（　　）

A．

（3，1），$4\sqrt{5}$

B．

（2，1），$4\sqrt{5}$

C．

（-3，1），$4\sqrt{3}$

D．

（2，-1），3$\sqrt{3}$

14．已知函数f（x）=ax²-（a+2）x+lnx
（1）当a＞0时，若f（x）在区间[1，e]上的最小值为-2，求a的取值范围；
（2）若对任意x₁，x₂∈（0，+∞），x₁＜x₂，且f（x₁）+2x₁＜f（x₂）+2x₂恒成立，求a的取值范围．

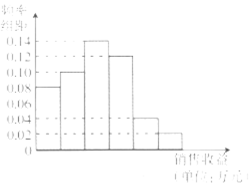13．某公司为了解广告投入对销售收益的影响，在若干地区各投入万元广告费用，并将各地的销售收益绘制成频率分布直方图（如图所示）．由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从开始计数的．
（Ⅰ）根据频率分布直方图计算图中各小长方形的宽度；
（Ⅱ）估计该公司投入万元广告费用之后，对应销售收益的平均值（以各组的区间中点值代表该组的取值）；
（Ⅲ）该公司按照类似的研究方法，测得另外一些数据，并整理得到下表：

广告投入x（单位：万元）	1	2	3	4	5
销售收益y（单位：万元）	2	3	2		7

表中的数据显示，与y之间存在线性相关关系，请将（Ⅱ）的结果填入空白栏，并计算y关于的回归方程．
回归直线的斜率和截距的最小二乘估计公式分别为$\frac{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．