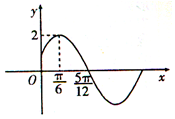14．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，$-\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示．
（1）求函数f（x）的解析式
（2）如何由函数y=2sinx的图象通过适当的变换得到函数f（x）的图象，写出变换过程．

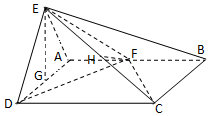13．如图所示，平面EAD⊥平面ABCD，△ADE是等边三角形，ABCD是矩形，F是AB的中点，P是O的中点，O是PQ的中点，EC与平面ABCD成30°角．
（1）求证：EG⊥平面ABCD；
（2）求证：HF∥平面EAD；
（3）若AD=4，求三棱锥D-CEF的体积．

12．已知椭圆${C_1}：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点分别为F₁，F₂，且F₂为抛物线${C_2}：{y^2}=2px$的焦点，C₂的准线l被C₁和圆x²+y²=a²截得的弦长分别为$2\sqrt{2}$和4．
（1）求C₁和C₂的方程；
（2）直线l₁过F₁且与C₂不相交，直线l₂过F₂且与l₁平行，若l₁交C₁于A，B，l₂交C₁交于C，D，且在x轴上方，求四边形AF₁F₂C的面积的取值范围．

11．过原点O作圆x²+y²-8x=0的弦OA，延长OA到N，使|OA|=|AN|，求点N的轨迹方程．

10．已知集合A={x|（x-1）（3-x）＜0}，B={x|-3≤x≤3}，则A∩B=（　　）

A．

（-1，2]

B．

（1，2]

C．

[-2，1）

D．

[-3，1）

9．设抛物线y²=-12x上一点P到y轴的距离是1，则点P到该抛物线焦点的距离是4．

8．已知全集U=R，集合A={x|x²-x-2≥0}，B={x|log₃x＜1，则（∁_UA）∩B=（　　）

A．

[2，3）

B．

[-1，2）

C．

（0，1）

D．

（0，2）

7．雾霾天气对人体健康有害，应对雾霾污染、改善空气质量是当前的首要任务是控制PM2.5，要从压减燃煤、严格控产、调整产业、强化管理、联防联控、依法治理等方面采取重大举措，聚焦重点领域，严格考核指标．某省环保部门为加强环境执法监管，派遣四个不同的专家组对A，B，C三个城市进行雾霾落实情况抽查．
（1）若每个专家组随机选取一个城市，四个专家组选取的城市可以相同，也可以不同，且每个城市都必须由专家组选取，求A城市恰有两有专家组选取的概率；
（2）在检查的过程中专家组从A城市的居民中随机抽取出400人进行是否户外作业人员与是否患有呼吸道疾病进行了统计，统计结果如下：

分类	患呼吸道疾病	未患呼吸道疾病	合计
户外作业人员	40	60	100
非户外作业人员	60	240	300
合计	100	300	400

根据上述的统计结果，我们是否有超过99%的把握认为“户外作业”与“患有呼吸道疾病”有关？
K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$

P（K2≥k）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	0.072	2.706	3.841	5.024	6.635	7.879	10.828

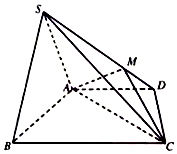6．如图，在四棱锥S-ABCD中，底面梯形ABCD中，AD∥BC，平面SAB⊥平面ABCD，△SAB是等边三角形，已知$AC=2AB=4，BC=2AD=2CD=2\sqrt{5}$，M是SD上任意一点，$\overrightarrow{SM}=m\overrightarrow{MD}$，且m＞0．
（1）求证：平面SAB⊥平面MAC；
（2）试确定m的值，使三棱锥S-ABC体积为三棱锥S-MAC体积的3倍．

5．已知正数数列{a_n}的前n项和为S_n，满足a_n²=S_n+S_n-1（n≥2），a₁=1．
（1）求数列{a_n}的通项公式；
（2）设b_n=（1-a_n）²-a（1-a_n），若b_n+1＞b_n对任意n∈N^*恒成立，求实数a的取值范围．