练习册

  • 练习册
  • 试题
    相关习题
     0  238067  238075  238081  238085  238091  238093  238097  238103  238105  238111  238117  238121  238123  238127  238133  238135  238141  238145  238147  238151  238153  238157  238159  238161  238162  238163  238165  238166  238167  238169  238171  238175  238177  238181  238183  238187  238193  238195  238201  238205  238207  238211  238217  238223  238225  238231  238235  238237  238243  238247  238253  238261  266669 

    科目： 来源： 题型：填空题

    4．已知函数f（x）=ex+ln（x+1）的图象在（0，f（0））处的切线与直线x-ny+4=0垂直，则n的值为-2．

    查看答案和解析>>

    科目： 来源： 题型：解答题

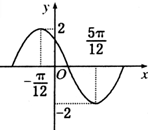    3．已知函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜π）在一个周期内的图象如图所示．
    （1）求函数f（x）的解析式与单调递减区间；
    （2）函数f（x）的图象上所有点的横坐标扩大到原来的2倍，再向右平移$\frac{π}{2}$个单位长度，得到g（x）的图象，求函数y=g（x）在x∈[0，π]上的最大值及最小值．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    2．实轴长为4$\sqrt{5}$，且焦点为（±5，0）的双曲线的标准方式为（　　）
    A．$\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1B．$\frac{{y}^{2}}{20}$-$\frac{{x}^{2}}{5}$=1C．$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{20}$=1D．$\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{25}$=1

    查看答案和解析>>

    科目： 来源： 题型：选择题

    1．双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1的离心率是（　　）
    A．$\frac{3}{5}$B．$\frac{5}{3}$C．$\frac{\sqrt{41}}{5}$D．$\frac{5}{\sqrt{41}}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    20．下列说法正确的是（　　）
    A．“sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件
    B．命题“若xy=0，则x=0或y=0”的否命题是“若xy≠0，则x≠0或y≠0”
    C．已知命题p：?x∈R，使2x＞3x；命题q：?x∈（0，+∞），都有$\frac{1}{{x}^{2}}$＜$\frac{1}{{x}^{3}}$，则p∧（￢q）是真命题
    D．从匀速传递的生产流水线上，质检员每隔5分钟从中抽取一件产品进行某项指标检测，这是分层抽样

    查看答案和解析>>

    科目： 来源： 题型：填空题

    19．已知函数$f（x）=sin2x+2{sin^2}\frac{1}{2}x$，则$f（\frac{π}{2017}）+f（\frac{2π}{2017}）+f（\frac{3π}{2017}）+…+f（\frac{2016π}{2017}）$=2016．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．已知sinα+cosα=$\frac{1}{5}$   且 0＜α＜π求：
    （1）sinαcosα；
    （2）tanα．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．已知函数$f（x）=\frac{1}{2}a{x^2}+lnx+bx$，其中a，b∈R．
    （1）当b=1时，g（x）=f（x）-x在$x=\frac{{\sqrt{2}}}{2}$处取得极值，求函数f（x）的单调区间；
    （2）若a=0时，函数f（x）有两个不同的零点x1，x2，
    ①求b的取值范围；
    ②求证：$\frac{{{x_1}{x_2}}}{e^2}＞1$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的一个顶点的坐标为（0，-1），且右焦点F到直线x-y+1=0的距离为$\sqrt{2}$．
    （1）求椭圆C的标准方程；
    （2）是否存在斜率为2的直线l，使得当直线l与椭圆C有两个不同交点M，N时，能在直线$y=\frac{5}{3}$上找到一点P，在椭圆C上找到一点Q，满足$\overrightarrow{PM}=\overrightarrow{NQ}$？若存在，求出直线l的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．已知函数f（x）=x2+mx+n，其中1≤m≤3，0≤n≤4，记函数f（x）满足条件$\left\{\begin{array}{l}f（2）≤12\\ f（-1）≤3\end{array}\right.$的事件为A，则事件A发生的概率为（　　）
    A．$\frac{5}{8}$B．$\frac{13}{16}$C．$\frac{3}{8}$D．$\frac{1}{2}$

    查看答案和解析>>

    同步练习册答案