练习册

  • 练习册
  • 试题
    相关习题
     0  238168  238176  238182  238186  238192  238194  238198  238204  238206  238212  238218  238222  238224  238228  238234  238236  238242  238246  238248  238252  238254  238258  238260  238262  238263  238264  238266  238267  238268  238270  238272  238276  238278  238282  238284  238288  238294  238296  238302  238306  238308  238312  238318  238324  238326  238332  238336  238338  238344  238348  238354  238362  266669 

    科目： 来源： 题型：选择题

    2．下面程序框图输出的结果是（　　）
    A．3B．12C．60D．360

    查看答案和解析>>

    科目： 来源： 题型：填空题

    1．直角坐标平面上一机器人在行进中始终保持到两点A（a，0）和B（0，1）的距离相等，且机器人也始终接触不到直线L：y=x+1，则a的值为1．

    查看答案和解析>>

    科目： 来源： 题型：选择题

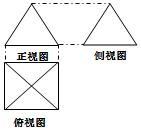    20．如果一个几何体的三视图如图所示，正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形，（单位长度：cm），则此几何体的侧面积是（　　）
    A．.$2\sqrt{3}$cmB．.$4\sqrt{3}$cm2C．8 cm2D．12 cm2

    查看答案和解析>>

    科目： 来源： 题型：选择题

    19．观察：$\sqrt{6}$+$\sqrt{15}$＜2$\sqrt{11}$，$\sqrt{5.5}$+$\sqrt{15.5}$＜2$\sqrt{11}$，$\sqrt{4-\sqrt{2}}$+$\sqrt{17+\sqrt{2}}$＜2$\sqrt{11}$，…，对于任意的正实数a，b，使$\sqrt{a}$+$\sqrt{b}$＜2$\sqrt{11}$成立的一个条件可以是（　　）
    A．a+b=22B．a+b=21C．ab=20D．ab=21

    查看答案和解析>>

    科目： 来源： 题型：填空题

    18．满足条件AB=2，AC=$\sqrt{3}$BC的三角形ABC面积的最大值是$\sqrt{3}$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    17．若函数f（x）=x2（x-a）在（2，3）上不单调，则实数a的取值范围是（3，$\frac{9}{2}$）．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    16．下列推理是演绎推理的是（　　）
    A．由 ${a_1}=1，{a_{n+1}}=\frac{a_n}{{1+{a_n}}}$，因为${a_1}=1，{a_2}=\frac{1}{2}，{a_3}=\frac{1}{3}，{a_4}=\frac{1}{4}$，故有${a_n}=\frac{1}{n}（n∈{N^*}）$
    B．科学家利用鱼的沉浮原理制造潜艇
    C．妲己惑纣王，商灭；西施迷吴王，吴灭；杨贵妃迷唐玄宗，致安史之乱，故曰：“红颜祸水也”
    D．《论语•学路》篇中说：“名不正，则言不顺；言不顺，则事不成；事不成，则礼乐不兴；礼乐不兴，则刑罚不中；刑罚不中，则民无所措手足；所以，名不正，则民无所措手足”．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    15．已知$α，β∈（{0，\frac{π}{2}}）$，且$α+β≠\frac{π}{2}，sinβ=sinαcos（{α+β}）$．
    （1）用tanα表示tanβ；
    （2）求tanβ的最大值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，离心率e=$\frac{\sqrt{2}}{2}$，且过点$（{1，\frac{{\sqrt{2}}}{2}}）$，
    （1）求椭圆的标准方程；
    （2）直线l：y=k（x+1）与该椭圆交于M、N两点，且|$\overrightarrow{{F}_{2}M}$+$\overrightarrow{{F}_{2}N}$|=$\frac{2\sqrt{26}}{3}$，求直线l的方程．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    13．设函数$f（x）=\frac{x}{x+2}（x＞0）$，观察：${f_1}（x）=f（x）=\frac{x}{x+2}$，${f_2}（x）=f（{f_1}（x））=\frac{x}{3x+4}$，${f_3}（x）=f（{f_2}（x））=\frac{x}{7x+8}$，${f_4}（x）=f（{f_3}（x））=\frac{x}{15x+16}$，…，根据以上事实，当n∈N*时，由归纳推理可得：fn（1）=$\frac{1}{{{2^{n+1}}-1}}$．

    查看答案和解析>>

    同步练习册答案