12．已知集合A={x|（x-2）（x+3）＜0}，B={x|y=$\sqrt{\frac{1}{x+1}}$}，则A∩（∁_RB）=（　　）

A．

[-3，-1]

B．

（-3，-1]

C．

（-3，-1）

D．

[-1，2]

11．已知函数f（x）=|mx+1|-|x-1|．
（Ⅰ）若m=1，求函数f（x）的最大值；
（Ⅱ）若m=-2，解不等式f（x）≥1．

10．设函数f（x）=alnx+$\frac{e}{x}$（e为自然对数的底数）．
（Ⅰ）当a＞0时，求函数f（x）的极值；
（Ⅱ）若不等式f（x）＜0在区间（0，e²]内有解，求实数a的取值范围．

9．已知抛物线C：y²=4x，直线x=ny+4与抛物线C交于A，B两点．
（Ⅰ）求证：$\overrightarrow{OA}$•$\overrightarrow{OB}$=0（其中O为坐标原点）；
（Ⅱ）设F为抛物线C的焦点，直线l₁为抛物线C的准线，直线l₂是抛物线C的通径所在的直线，过C上一点P（x₀，y₀）（y₀≠0）作直线l：y₀y=2（x+x₀）与直线l₂相交于点M，与直线l₁相交于点N，证明：点P在抛物线C上移动时，$\frac{|MF|}{|NF|}$恒为定值，并求出此定值．

8．某种新产品投放市场一段时间后，经过调研获得了时间x（天数）与销售单价y（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）．

$\overline{x}$	$\overline{y}$	$\overline{w}$	$\sum_{i=1}^{10}（{x}_{i}-\overline{x}）^{2}$	$\sum_{i=1}^{10}（{w}_{i}-\overline{w}）^{2}$	$\sum_{i=1}^{10}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）$	$\sum_{i=1}^{10}（{w}_{i}-\overline{w}）（{y}_{i}-\overline{y}）$
1.63	37.8	0.89	5.15	0.92	-20.6	18.40

表中w_i=$\frac{1}{{x}_{i}}$，$\overline{w}$=$\frac{1}{10}$$\sum_{i=1}^{10}{w}_{i}$．
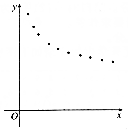（Ⅰ）根据散点图判断，$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x与$\widehat{y}$=$\widehat{c}$+$\frac{\widehat{d}}{x}$哪一个更适宜作价格y关于时间x的回归方程类型？（不必说明理由）
（Ⅱ）根据判断结果和表中数据，建立y关于x的回归方程；
（Ⅲ）若该产品的日销售量g（x）（件）与时间x的函数关系为g（x）=$\frac{-100}{x}$+120（x∈N^*），求该产品投放市场第几天的销售额最高？最高为多少元？
附：对于一组数据（u₁，v₁），（u₂，v₂），（u₃，v₃），…，（u_n，v_n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{v}_{i}-\overline{v}）（{u}_{i}-\overline{u}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．

7．如图，在三棱锥ABC-A₁B₁C₁中，△ABC是边长为2的等边三角形，AA₁=4，A₁在底面ABC上的射影为BC的中点E，D是B₁C₁的中点．
（Ⅰ）证明：A₁D⊥A₁C；
（Ⅱ）求三棱柱ABC-A₁B₁C₁的体积．

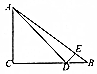6．如图，在△ABC中，角A，B，C的对边分别为a，b，c，C=$\frac{π}{2}$，D，E分别为BC，AB上的点，∠ADC=∠EDB=$\frac{π}{4}$，DB=$\sqrt{2}$，AE=3EB，则边长AC的值为$\frac{3\sqrt{2}}{2}$．

5．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+2y≥0，}&{\;}\\{x-y≤0，}&{\;}\\{x-2y+2≥0，}&{\;}\end{array}\right.$则（x+3）²+（y-$\frac{1}{2}$）²的最小值为4．

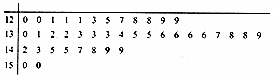4．在高三某次数学测试中，40名优秀学生的成绩如图所示：
若将成绩由低到高编为1～40号，再用系统抽样的方法从中抽取8人，则其中成绩在区间[123，134]上的学生人数为3．

3．已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则当x∈[-1，1]时，函数f（x）的值域为（　　）

A．

[-1，$\frac{\sqrt{2}}{2}$]

B．

[$\frac{\sqrt{2}}{2}$，1]

C．

[-$\frac{\sqrt{2}}{2}$，1]

D．

[-1，1]