练习册

  • 练习册
  • 试题
    相关习题
     0  238275  238283  238289  238293  238299  238301  238305  238311  238313  238319  238325  238329  238331  238335  238341  238343  238349  238353  238355  238359  238361  238365  238367  238369  238370  238371  238373  238374  238375  238377  238379  238383  238385  238389  238391  238395  238401  238403  238409  238413  238415  238419  238425  238431  238433  238439  238443  238445  238451  238455  238461  238469  266669 

    科目： 来源： 题型：解答题

    5．设三个各项均为正整数的无穷数列{an}，{bn}，{cn}．记数列{bn}，{cn}的前n项和分别为Sn，Tn，若对任意的n∈N*，都有an=bn+cn，且Sn＞Tn，则称数列{an}为可拆分数列．
    （1）若${a_n}={4^n}$，且数列{bn}，{cn}均是公比不为1的等比数列，求证：数列{an}为可拆分数列；
    （2）若an=5n，且数列{bn}，{cn}均是公差不为0的等差数列，求所有满足条件的数列{bn}，{cn}的通项公式；
    （3）若数列{an}，{bn}，{cn}均是公比不为1的等比数列，且a1≥3，求证：数列{an}为可拆分数列．

    查看答案和解析>>

    科目： 来源： 题型：解答题

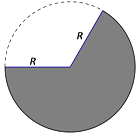    4．某工厂要生产体积为定值V的漏斗，现选择半径为R的圆形马口铁皮，截取如图所示的扇形，焊制成漏斗．
    （1）若漏斗的半径为$\frac{\sqrt{3}}{2}$R，求圆形铁皮的半径R；
    （2）这张圆形铁皮的半径R至少是多少？

    查看答案和解析>>

    科目： 来源： 题型：解答题

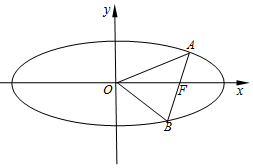    3．如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2，过右焦点F的直线l交椭圆于A、B两点，当l与x轴垂直时，AB长为$\frac{{4\sqrt{3}}}{3}$．   
    （1）求椭圆的标准方程；
    （2）若椭圆上存在一点P，使得$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$，求直线l的斜率．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    2．如图，在四棱锥P-ABCD中，四边形ABCD为矩形，AB⊥BP，M为AC的中点，N为PD上一点．
    （1）若MN∥平面ABP，求证：N为PD的中点；
    （2）若平面ABP⊥平面APC，求证：PC⊥平面ABP．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    1．在平面直角坐标系xOy中，以Ox轴为始边，作两个角α，β，它们终边分别经过点P，Q，其中$P（\frac{1}{2}，{cos^2}θ）$，Q（sin2θ，-1），θ∈R，且$sinα=\frac{4}{5}$．
    （1）求cos2θ的值；
    （2）求tan（α+β）的值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    20．已知如表为“五点法”绘制函数f（x）=Asin（ωx+φ）图象时的五个关键点的坐标（其中A＞0，ω＞0，|φ|＜π）．
    x$-\frac{π}{6}$$\frac{π}{12}$$\frac{π}{3}$$\frac{7π}{12}$$\frac{5π}{6}$
    f（x）020-20
    （Ⅰ） 请写出函数f（x）的解析式，并求函数f（x）的单调递增区间；
    （Ⅱ） 求函数f（x）在区间$[0，\frac{π}{2}]$上的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    19．△ABC中，角A，B，C所对的边分别为a，b，c，且满足3bcosC=3a-c，则cosB=（　　）
    A．$\frac{2\sqrt{2}}{3}$B．$\frac{1}{3}$C．-$\frac{2\sqrt{2}}{3}$D．-$\frac{1}{3}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．在△ABC中，角A，B，C的对边分别为a，b，c，已知$a{cos^2}\frac{B}{2}+b{cos^2}\frac{A}{2}=\frac{3}{2}c，a=2b$．
    （1）证明：△ABC为钝角三角形；
    （2）若△ABC的面积为$3\sqrt{15}$，求b的值．

    查看答案和解析>>

    科目： 来源： 题型：填空题

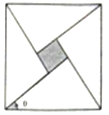    17．我国古代数学家赵爽利用“勾股圈方图”巧妙的证明了勾股定理，成就了我国古代数学的骄傲，后人称之为“赵爽弦图”．他是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形，若直角三角形中较小的锐角记为θ，大正方形的面积为25，小正方形的面积为1，则$sin\frac{θ}{2}+cos\frac{θ}{2}$=$\frac{{2\sqrt{10}}}{5}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知函数f（x）=|x-2|．
    （1）若对任意的a，b，c∈R（a≠c），不等式$\frac{1}{2}$f（m）≤$\frac{|a-b|+|c-d|}{|a-c|}$恒成立，求实数m的最大值；
    （2）在（1）的条件下，解不等式f（x）≤2-|x-m|．

    查看答案和解析>>

    同步练习册答案