3．若sin（α+β）=2sin（α-β）=$\frac{1}{2}$，则sinαcosβ的值为（　　）

A．

$\frac{3}{8}$

B．

$-\frac{3}{8}$

C．

$\frac{1}{8}$

D．

$-\frac{1}{8}$

2．若$\overrightarrow{AB}$$•\overrightarrow{AC}$=-1，|$\overrightarrow{AB}$|=2，|$\overrightarrow{AC}$|=1，则（$\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AC}$）•（$\overrightarrow{AB}$+$\overrightarrow{AC}$）的值为（　　）

A．

$\frac{3}{8}$

B．

$\frac{3}{4}$

C．

$\frac{5}{4}$

D．

$\frac{3}{2}$

1．已知集合A={x|x²-x-6≥0}，B={x|-3≤x≤3}，则A∩B等于（　　）

A．

[-3，-2]

B．

[2，3]

C．

[-3，-2]∪{3}

D．

[2，3]∪{-3}

20．设复数z=1+bi（b∈R），且z²=-3+4i，则$\overline{z}$的虚部为（　　）

A．

-2

B．

-4

C．

2

D．

4

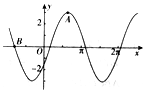19．已知函数f（x）=Msin（ωx+φ）（M＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，其中A（2，3）（点A为图象的一个最高点），B（-$\frac{5}{2}$，0），则函数f（x）=3sin（$\frac{π}{3}$x-$\frac{π}{6}$）．

18．国内某知名连锁店分店开张营业期间，在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效开展，参加抽奖活动的人数越来越多，该分店经理对开业前7天参加抽奖活动的人数进行统计，y表示开业第x天参加抽奖活动的人数，得到统计表格如下：

x	1	2	3	4	5	6	7
y	5	8	8	10	14	15	17

经过进一步统计分析，发现y与x具有线性相关关系．
（Ⅰ）若从这7天随机抽取两天，求至少有1天参加抽奖人数超过10的概率；
（Ⅱ）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$，并估计若该活动持续10天，共有多少名顾客参加抽奖．
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{x}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$，$\sum_{i-1}^{7}{x}_{i}^{2}$=140，$\sum_{i=1}^{7}{x}_{i}{y}_{i}$=364．

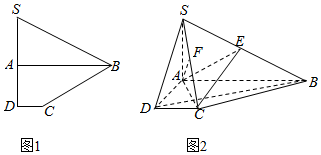17．如图（1）所示，已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的，其中∠SAB=∠SDC=90°，且点A为线段SD的中点，AD=2DC=1，AB=SD，现将△SAB沿AB进行翻折，使得二面角S-AB-C的大小为90°，得到的图形如图（2）所示，连接SC，点E、F分别在线段SB、SC上．
（Ⅰ）证明：BD⊥AF；
（Ⅱ）若三棱锥B-AEC的体积是四棱锥S-ABCD体积的$\frac{2}{5}$，求点E到平面ABCD的距离．

16．若圆C过点（0，-1），（0，5），且圆心到直线x-y-2=0的距离为2$\sqrt{2}$，则圆C的标准方程为x²+（y-2）²=9或（x-8）²+（y-2）²=73．

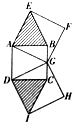15．折纸已经成为开发少年儿童智力的一大重要工具和手段．已知在折叠“爱心”的过程中会产生如图所示的几何图形，其中四边形ABCD为正方形，G为线段BC的中点，四边形AEFG与四边形DGHI也为正方形，连接EB，CI，则向多边形AEFGHID中投掷一点，该点落在阴影部分内的概率为$\frac{\sqrt{3}}{5}$．

14．已知命题p：?x∈（1，+∞），x³+16＞8x，则命题p的否定为（　　）

	A．	￢p：?x∈（1，+∞），x3+16≤8x		B．	￢p：?x∈（1，+∞），x3+16＜8x
	C．	￢p：?x0∈（1，+∞），x03+16≤8x0		D．	￢p：?x0∈（1，+∞），x03+16＜8x0