练习册

  • 练习册
  • 试题
    相关习题
     0  238468  238476  238482  238486  238492  238494  238498  238504  238506  238512  238518  238522  238524  238528  238534  238536  238542  238546  238548  238552  238554  238558  238560  238562  238563  238564  238566  238567  238568  238570  238572  238576  238578  238582  238584  238588  238594  238596  238602  238606  238608  238612  238618  238624  238626  238632  238636  238638  238644  238648  238654  238662  266669 

    科目： 来源： 题型：选择题

    19．在数列{an}中，a1=1，an+1=2an，${S_n}=a_1^2-a_2^2+a_3^2-a_4^2+$…$+a_{2n-1}^2-a_{2n}^2$等于（　　）
    A．$\frac{1}{3}（{2^n}-1）$B．$\frac{1}{5}（1-{2^{4n}}）$C．$\frac{1}{3}（{4^n}-1）$D．$\frac{1}{3}（1-{2^n}）$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    18．某几何体的三视图如图，则该几何体的体积为（　　）
    A．18B．20C．24D．12

    查看答案和解析>>

    科目： 来源： 题型：选择题

    17．将直角三角形ABC沿斜边上的高AD折成120°的二面角，已知直角边AB=4$\sqrt{3}$，AC=4$\sqrt{6}$，那么下面说法正确的是（　　）
    A．平面ABC⊥平面ACD
    B．四面体D-ABC的体积是$\frac{16}{3}\sqrt{6}$
    C．二面角A-BC-D的正切值是$\frac{{\sqrt{42}}}{5}$
    D．BC与平面ACD所成角的正弦值是$\frac{{\sqrt{21}}}{14}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    16．已知函数f（x）=2sinxsin（x+3φ）是奇函数，其中$φ∈（0，\frac{π}{2}）$，则函数g（x）=cos（2x-φ）的图象（　　）
    A．关于点$（\frac{π}{12}，0）$对称
    B．关于轴$x=-\frac{5π}{12}$对称
    C．可由函数f（x）的图象向右平移$\frac{π}{6}$个单位得到
    D．可由函数f（x）的图象向左平移$\frac{π}{3}$个单位得到

    查看答案和解析>>

    科目： 来源： 题型：解答题

    15．已知a＞0，b＞0，且$\sqrt{a}+\sqrt{b}=1$．
    （Ⅰ）求$\frac{1}{a}+\frac{1}{b}$的最小值；
    （Ⅱ）求a2b的最大值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．已知函数f（x）=ex-ax-1（a＞0）．
    （1）若f（x）≥0对任意的x∈R恒成立，求实数a的值；
    （2）在（1）的条件下，证明：（$\frac{1}{n}$）n+（$\frac{2}{n}$）n+…+（$\frac{n-1}{n}$）n+（$\frac{n}{n}$）n＜$\frac{e}{e-1}$（n∈N*）．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    13．已知区域D：{（x，y）||y|≤|x|}，则（　　）
    A．?x0＞0，（x0，$\frac{1}{2}$）∈DB．?x0＞0，（x0，$\frac{1}{2}$x0）∉DC．?x0＞0，（x0，$\frac{1}{2}$）∈DD．?x0＞0，（x0，$\frac{1}{2}$x0）∉D

    查看答案和解析>>

    科目： 来源： 题型：解答题

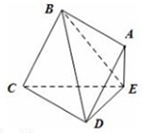    12．边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD，且AE⊥平面CDE．
    （Ⅰ）求证：平面ABCD⊥平面ADE；
    （Ⅱ）若三棱锥A-BDE的体积为$\frac{\sqrt{3}}{3}$，求AE长．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    11．如图，在一段直行的公路上方D处有一测速球机，在球机下方路面有A，B，C三个测速点，测得球机距点A为14米，AB=10米，球机探测点B和C的俯角分别为60°和45°，现有一小汽车从A地到C地用时1秒，则小汽车经过AC这段路程的平均速度约为18.1米/秒．（结果精确到0.1，参考数据$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．已知点P是抛物线y2=4x上的一点，抛物线的焦点为F，若|PF|=5，直线PF的斜率为k，则|k|=$\frac{4}{3}$．

    查看答案和解析>>

    同步练习册答案