19．$\frac{（x+y+1）^{5}}{xy}$展开式中的常数项为（　　）

A．

20

B．

10

C．

5

D．

1

18．各项均不为零的等差数列{a_n}的前n项和为S_n，则$\frac{{S}_{5}}{{a}_{3}}$的值是（　　）

A．

$\frac{1}{2}$

B．

1

C．

$\frac{5}{2}$

D．

5

17．已知集合A={x|x＞0}，B={x|x²-2x-3＜0}，则A∩B=（　　）

A．

（-1，0）

B．

（0，3）

C．

（-∞，0）∪（3，+∞）

D．

（-1，3）

16．设f（x）=|x+a|-|x+1|．
（Ⅰ）求不等式f（a）＞1的解集；
（Ⅱ）当x∈R时，f（x）≤2a（a∈R），求实数a的取值范围．

15．已知函数f（x）=x²lnax（a＞0）．
（Ⅰ）求函数y=f（x）的单调区间；
（Ⅱ）当a=e时，证明：t＞0时，存在唯一的s，使ts²+t²=f（s）．

14．经统计，2015年，某公路在部分界桩附近发生的交通事故次数如下表：

界桩公里数  1001	1005	1010	1020	1025	1049
交通事故数  80	40	35	33	32	30

（Ⅰ）把界桩公里数1001记为x=1，公里数1005记为x=5，…，数据绘成的散点图如图所示，以x为解释变量、交通事故数y为预报变量，请在y=a+be^-x和y=a+$\frac{b}{x}$间选取一个建立回归方程表述x，y二者之间的关系（a，b的值精确到0.1）；
（Ⅱ）若保险公司在2015年交通事故中随机抽取100例，理赔60万元的有1例，理赔2万元的有19例，理赔0.2万元的有80例．
      利用你得到的回归方程，试预报这一年在界桩1040公里附近处发生的交通事故的理赔费（理赔费精确到0.1万元）．
附：回归直线v=$\widehat{α}$+$\widehat{β}$u的斜率和截距的最小二乘法估计分别为：
$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．
一些量的计算值：

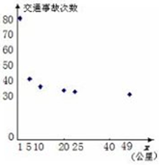
$\overline{x}$	$\overline{y}$        $\overline{ω}$        $\overline{φ}$	$\sum_{i=1}^{6}（{ω}_{i}-\overline{ω}）^{2}$	$\sum_{i=1}^{6}（{φ}_{i}-\overline{φ}）^{2}$	$\sum_{i=1}^{6}（{ω}_{i}-\overline{ω}）（{y}_{i}-\overline{y}）$	$\sum_{i=1}^{6}（{φ}_{i}-\overline{φ}）（{y}_{i}-\overline{y}）$
18.3	41.7  0.235  0.062	0.723	0.112	36.3	14.1

表中：ω_i=$\frac{1}{{x}_{i}}$，$\overline{ω}$=$\frac{1}{6}$$\sum_{i=1}^{6}{ω}_{i}$；φ_i=e${\;}^{-{x}_{i}}$，$\overline{φ}$=$\frac{1}{6}$$\sum_{i=1}^{6}{φ}_{i}$，$\frac{1}{40}$=0.025，e^-40≈0．

13．已知a₁=$\frac{1}{2}$a₂≠0，数列{a_n}的前n项和为S_n，且S_n+1=3S_n-2S_n-1（n≥2），设b_n=$\frac{{S}_{n}}{{a}_{n}}$（n∈N^*）．
（1）求数列{b_n}的通项公式；
（2）设c_n=nb_n+$\frac{n+1}{{2}^{n}}$（n∈N^*），数列{c_n}的前n项和为T_n，证明：T₁₀＞109．

12．函数f（x）=xe^x+1的图象在点（0，f（0））处的切线方程是x-y+1=0．

11．设复数z=1+i，则复数z+$\frac{2}{z}$=2．

10．已知f（x）为偶函数，在[0，+∞）上f（x）=$\left\{\begin{array}{l}{a（{x}^{3}-1），x∈[0，1]}\\{x+\frac{a}{x}-2，x∈（1，+∞）}\end{array}\right.$且为单调递增函数，则使得f（ax）＞f（2x-1）成立的x的取值范围是（　　）

A．

（$\frac{1}{3}$，1）

B．

（-∞，$\frac{1}{3}$）∪（1，+∞）

C．

（-$\frac{1}{3}$，1）

D．

D、（-∞，$-\frac{1}{3}$）∪（$\frac{1}{3}$，+∞）