6．如图，在正方体ABCD-A₁B₁C₁D₁中，M，N分别为BC，BB₁的中点，求AB与平面AMN所成的角的正弦值．

5．写出分别满足下列条件的双曲线的标准方程．
（1）曲线上的点P到点F₁（4，0）的距离与它到点F₂（4，0）的距离的差的绝对值等于6．
（2）曲线上的点P到点F₁（-10，0）的距离与它到点F₂（10，0）的距离的差等于16．

4．若函数f（x）=e^x（sinx+acosx）在（$\frac{π}{4}$，$\frac{π}{2}$）上单调递增，则实数a的取值范围是（　　）

A．

（-∞，1]

B．

（-∞，1）

C．

[1，+∞）

D．

（1，+∞）

3．如图，约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$，若在可行域△ABC上有无穷多个点（x，y），使得目标函数z=x+my取得最小值，求m的值．

2．已知圆C：（x-3）²+（y-t）²=t²（t≠0，t∈R），A（-3，0），B（3，2t），F（2，0）．
（1）若过A倾斜角为60°的直线与圆C相切，求t的值；
（2）过F且倾斜角不为0的直线l与圆C相切，l与AB交于M，求点M的轨迹方程．

1．已知函数f（x）=ae^x-x²-（3a+1）x，若函数f（x）在区间（0，ln3）上有极值，则实数a的取值范围是（　　）

A．

（-∞，-$\frac{1}{2}$）

B．

（-∞，-1）

C．

（-1，-$\frac{1}{2}$）

D．

（-∞，-2）∪（0，1）

3．在△ABC中，若AB=$\sqrt{2}$，∠B=60°，△ABC的面积S=$\frac{\sqrt{3}+3}{4}$，则AC=（　　）

A．

$\sqrt{3}$

B．

$\sqrt{6}$

C．

2$\sqrt{2}$

D．

2$\sqrt{3}$

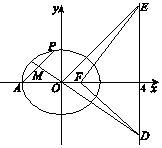2．如图，已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;（a＞b＞0）$的离心率为$\frac{1}{2}$，F为椭圆C的右焦点．A（-a，0），|AF|=3．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设O为原点，P为椭圆上一点，AP的中点为M．直线OM与直线x=4交于点D，过O且平行于AP的直线与直线x=4交于点E．求证：∠ODF=∠OEF．

1．在测试中，客观题难度的计算公式为${P_i}=\frac{R_i}{N}$，其中P_i为第i题的难度，R_i为答对该题的人数，N为参加测试的总人数．现对某校高三年级240名学生进行一次测试，共5道客观题．测试前根据对学生的了解，预估了每道题的难度，如表所示：

题号	1	2	3	4	5
考前预估难度Pi	0.9	0.8	0.7	0.6	0.4

测试后，随机抽取了20名学生的答题数据进行统计，结果如下：

题号	1	2	3	4	5
实测答对人数	16	16	14	14	4

（Ⅰ）根据题中数据，估计这240名学生中第5题的实测答对人数；
（Ⅱ）从抽样的20名学生中随机抽取2名学生，记这2名学生中第5题答对的人数为X，求X的分布列和数学期望；
（Ⅲ）试题的预估难度和实测难度之间会有偏差．设${P_i}^′$为第i题的实测难度，请用P_i和${P_i}^′$设计一个统计量，并制定一个标准来判断本次测试对难度的预估是否合理．

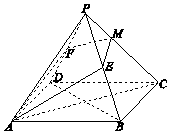20．如图，在正四棱锥P-ABCD中，PA=AB，E，F分别为PB，PD的中点．
（Ⅰ）求证：AC⊥平面PBD；
（Ⅱ）求异面直线PC与AE所成角的余弦值；
（Ⅲ）若平面AEF与棱PC交于点M，求$\frac{PM}{PC}$的值．