18．已知λ∈R，向量$\overrightarrow a=（{3，λ}）\;，\;\overrightarrow b=（{λ-1\;，\;2}）$，则“λ=3”是“$\overrightarrow a∥\overrightarrow b$”的（　　）

	A．	必要不充分条件		B．	充分不必要条件
	C．	充分必要条件		D．	即不充分也不必要条件

17．下列有关于f（x）=ln（1+|x|）-$\frac{1}{1{+x}^{2}}$的性质的描述，正确的是（　　）

	A．	奇函数，在R上单调递增
	B．	奇函数，在（-∞，0）上单调递增，在（0，+∞）上单调递增
	C．	偶函数，在（-∞，0）上单调递减，在（0，+∞）上单调递增
	D．	偶函数，在（-∞，0）上单调递增，在（0，+∞）上单调递减

16．若${（{x^2}-\frac{1}{x}）^n}$的展开式中含x³的项为第6项，设（1-3x）ⁿ=a₀+a₁x+a₂x²+…+a_nxⁿ，则a₁+a₂+…+a_n的值为-513．

15．我们知道，在长方形ABCD中，如果设AB=a，BC=b，那么长方形ABCD的外接圆的半径R满足4R²=a²+b²，类比上述结论，在长方体ABCD-A₁B₁C₁D₁中，如果设AB=a，AD=b，AA₁=c，那么长方体ABCD-A₁B₁C₁D₁的外接球的半径R满足的关系式是（　　）

A．

4R2=a3+b3+c3

B．

8R2=a2+b2+c2

C．

8R3=a3+b3+c3

D．

4R2=a2+b2+c2

14．已知两个变量x，y之间具有相关关系，现选用a，b，c，d四个模型得到相应的回归方程，并计算得到了相应的R²值分别为R_a²=0.80，R_b²=0.98，R_c²=0.93，R_d²=0.86，那么拟合效果最好的模型为（　　）

A．

a

B．

b

C．

c

D．

d

13．执行如图所示的程序框图，若输入n=10，则输出k的值为（　　）

A．

7

B．

6

C．

5

D．

4

12．阅读材料：根据两角和与差的正弦公式，有：
sin（α+β）=sinαcosβ+cosαsinβ------①
sin（α-β）=sinαcosβ-cosαsinβ------②
由①+②得sin（α+β）+sin（α-β）=2sinαcosβ------③
令α+β=A，α-β=β　有α=$\frac{A+B}{2}$，β=$\frac{A-B}{2}$代入③得　sinA+sinB=2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$．
（1）利用上述结论，试求sin15°+sin75°的值；
（2）类比上述推证方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$．

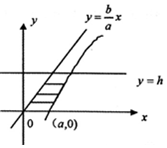11．我们在学习立体几何推导球的体积公式时，用到了祖暅原理：即两个等高的几何体，被等高的截面所截，若所截得的面积总相等，那么这两个几何体的体积相等．类比此方法：求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0），与x轴，直线y=h（h＞0）及渐近线y=$\frac{b}{a}$x所围成的阴影部分（如图）绕y轴旋转一周所得的几何体的体积a²hπ．

10．用数学归纳法证明不等式1+$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n-1}}$＞$\frac{127}{64}$成立，起始值应取为n=8．

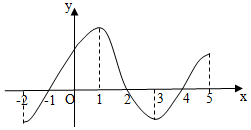9．如图是函数y=f（x）的导数的图象，则正确的判断是（2）（4）．
（1）f（x）在（-2，1）上是增函数；
（2）x=-1是f（x）的极小值点；
（3）x=2是f（x）的极小值点；
（4）f（x）在（2，4）上是减函数，在（-1，2）上是增函数．