练习册

  • 练习册
  • 试题
    相关习题
     0  238630  238638  238644  238648  238654  238656  238660  238666  238668  238674  238680  238684  238686  238690  238696  238698  238704  238708  238710  238714  238716  238720  238722  238724  238725  238726  238728  238729  238730  238732  238734  238738  238740  238744  238746  238750  238756  238758  238764  238768  238770  238774  238780  238786  238788  238794  238798  238800  238806  238810  238816  238824  266669 

    科目： 来源： 题型：填空题

    2．已知向量$\overrightarrow{a}$=（x，y）（x，y∈R），$\overrightarrow{b}$=（1，2），若x2+y2=1，则|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值为$\sqrt{5}$-1．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    1．直线2x-y+a=0与3x+y-3=0交于第一象限，当点P（x，y）在不等式组$\left\{\begin{array}{l}{2x-y+a≥0}\\{3x+y-3≤0}\end{array}\right.$表示的区域上运动时，m=4x+3y的最大值为8，此时n=$\frac{y}{x+3}$的最大值是（　　）
    A．$\frac{1}{4}$B．$\frac{3}{2}$C．$\frac{4}{3}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    20．已知函数f（x）=$\left\{\begin{array}{l}{（lnx）^{2}+alnx+b，x＞0}\\{{e}^{x}+\frac{1}{4}，x≤0}\end{array}\right.$，且f（e）=f（1），f（e2）=f（0）+$\frac{11}{4}$，则函数f（x）的值域为（　　）
    A．（$\frac{1}{4}$，$\frac{5}{4}$]∪（$\frac{7}{4}$，+∞）B．（$\frac{1}{4}$，$\frac{7}{4}$）C．（-∞，$\frac{1}{4}$]∪[$\frac{5}{4}$，+∞）D．（$\frac{1}{4}$，$\frac{5}{4}$]∪[$\frac{7}{4}$，+∞）

    查看答案和解析>>

    科目： 来源： 题型：选择题

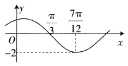    19．已知函数f（x）=Asin（wx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（　　）
    A．g（x）=2sin（2x-$\frac{π}{3}$）B．g（x）=2sin（2x+$\frac{π}{6}$）C．g（x）=-2sin（2x-$\frac{π}{3}$）D．g（x）=-2sin（2x+$\frac{π}{6}$）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    18．已知点F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，过F点作双曲线的一条渐近线垂线，垂足为A，交另一条渐近线于B，若A点恰好为BF的中点，则双曲线的离心率为（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．2D．3

    查看答案和解析>>

    科目： 来源： 题型：选择题

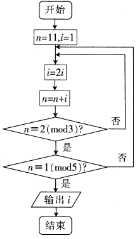    17．《孙子算经》是中国公元四世纪的数学著作，其中接受了求解依次同余式的方法，他是数论中一个重要的定理，又称《中国剩余定理》，如图所示的程序框图的算法就是源于《中国剩余定理》，执行该程序框图，若正整数N除以正整数m后的余数为n，则记为N≡n（modm），例如11≡3（mod4），则输出的等于（　　）
    A．8B．16C．32D．64

    查看答案和解析>>

    科目： 来源： 题型：选择题

    16．若复数z=$\frac{2}{1+i}$+（1-i）2，则|z|等于（　　）
    A．$\sqrt{10}$B．$\sqrt{2}$C．2D．$\sqrt{5}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    15．在平面直角坐标系xOy中曲线${C_1}：{x^2}+{y^2}=1$经伸缩变换$\left\{{\begin{array}{l}{{x^2}=2x}\\{{y^2}=y}\end{array}}\right.$后得到曲线C2，在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C3的极坐标方程为$ρ=\frac{-8}{ρ-6sinθ}$．
    （1）求曲线C2的参数方程和C3的直角坐标方程；
    （2）设M为曲线C2上的一点，又M向曲线C3引切线，切点为N，求|MN|的最大值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．如图，四边形ABCD中，△BCD为正三角形，AD=AB=2，$BD=2\sqrt{3}$，AC与BD中心O点，将△ACD沿边AC折起，使D点至P点，已知PO与平面ABCD所成的角为60°．
    （1）求证：平面PAC⊥平面PDB；
    （2）求已知二面角A-PB-D的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    13．已知数列{an}满足${a_1}{a_2}{a_3}…{a_n}={2^{n^2}}$（n∈N*），且对任意n∈N*都有$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_n}＜t$，则实数t的取值范围为$[\frac{2}{3}，+∞）$．

    查看答案和解析>>

    同步练习册答案