18．已知两点A（-1，1），B（3，5），点C在曲线y=2x²上运动，则$\overrightarrow{AB}•\overrightarrow{AC}$的最小值为（　　）

A．

2

B．

$\frac{1}{2}$

C．

-2

D．

$-\frac{1}{2}$

17．已知命题p：?x∈R，x²+ax+a²≥0（a∈R），命题q：$?{x_0}∈{N^*}$，$2x_0^2-1≤0$，则下列命题中为真命题的是（　　）

A．

p∧q

B．

p∨q

C．

（?p）∨q

D．

（?p）∧（?q）

16．已知集合A={-1，0，1，2，3，4，5}，B={b|b=n²-1，n∈Z}，则A∩B=（　　）

A．

{-1，3}

B．

{0，3}

C．

{-1，0，3}

D．

{-1，0，3，5}

15．点M为椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$上一点，则M到直线的距离x+2y-10=0最小值为（　　）

A．

$3\sqrt{5}$

B．

$2\sqrt{5}$

C．

$\sqrt{5}$

D．

$\frac{{\sqrt{5}}}{2}$

14．已知函数f（x）=|x+3|+|x-1|的最小值为m．
（Ⅰ）求m的值以及此时的x的取值范围；
（Ⅱ）若实数p，q，r满足p²+2q²+r²=m，证明：q（p+r）≤2．

13．已知函数$f（x）=\frac{lnx}{x}$，g（x）=e^x．
（Ⅰ）若关于x的不等式f（x）≤mx≤g（x）恒成立，求实数m的取值范围；
（Ⅱ）若x₁＞x₂＞0，求证：[x₁f（x₁）-x₂f（x₂）]$（{x_1^2+x_2^2}）$＞2x₂（x₁-x₂）．

12．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{1}{2}$，且过点$（{-1，\frac{3}{2}}）$，椭圆C的右顶点为A．
（Ⅰ）求椭圆的C的标准方程；
（Ⅱ）已知过点$B（{\frac{1}{2}，0}）$的直线交椭圆C于P，Q两点，且线段PQ的中点为R，求直线AR的斜率的取值范围．

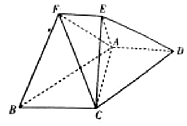11．已知多面体ABCDEF中，四边形ABCD为平行四边形，AD⊥平面AEC，且$AC=\sqrt{2}$，AE=EC=1，AD=2EF，EF∥AD．
（Ⅰ）求证：平面FCE⊥平面ADE；
（Ⅱ）若AD=2，求多面体ABCDEF的体积．

10．为了更好地规划进货的数量，保证蔬菜的新鲜程度，某蔬菜商店从某一年的销售数据中，随机抽取了8组数据作为研究对象，如图所示（x（吨）为买进蔬菜的质量，y（天）为销售天数）：

x	2	3	4	5	6	7	9	12
y	1	2	3	3	4	5	6	8

（Ⅰ）根据上表数据在下列网格中绘制散点图；
（Ⅱ）根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$；
（Ⅲ）根据（Ⅱ）中的计算结果，若该蔬菜商店准备一次性买进25吨，则预计需要销售多少天．
参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）}（{{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．

9．已知△ABC中，角A，B，C所对的边分别是a，b，c，$sinA=\sqrt{3}sinC$，$b=\sqrt{7}$．
（Ⅰ）若$B=\frac{π}{6}$，证明：sinB=sinC；
（Ⅱ）若B为钝角，$cos2B=\frac{1}{2}$，求AC边上的高．