15．在平面直角坐标系xOy中，抛物线C的顶点是原点，以x轴为对称轴，且经过点P（1，2）．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设点A，B在抛物线C上，直线PA，PB分别与y轴交于点M，N，|PM|=|PN|．求直线AB的斜率．

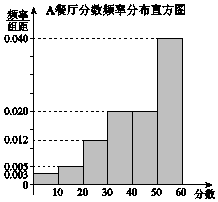14．某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．整理评分数据，将分数以10为组距分成6组：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：

B餐厅分数频数分布表
分数区间	频数
[0，10）	2
[10，20）	3
[20，30）	5
[30，40）	15
[40，50）	40
[50，60]	35

定义学生对餐厅评价的“满意度指数”如下：

分数	[0，30）	[30，50）	[50，60]
满意度指数	0	1	2

（Ⅰ）在抽样的100人中，求对A餐厅评价“满意度指数”为0的人数；
（Ⅱ）从该校在A，B两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．

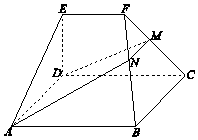13．如图，在几何体ABCDEF中，底面ABCD为矩形，EF∥CD，AD⊥FC．点M在棱FC上，平面ADM与棱FB交于点N．
（Ⅰ）求证：AD∥MN；
（Ⅱ）求证：平面ADMN⊥平面CDEF；
（Ⅲ）若CD⊥EA，EF=ED，CD=2EF，平面ADE∩平面BCF=l，求二面角A-l-B的大小．

12．已知函数$f（x）=tan（x+\frac{π}{4}）$．
（Ⅰ）求f（x）的定义域；
（Ⅱ）设β∈（0，π），且$f（β）=2cos（β-\frac{π}{4}）$，求β的值．

11．设$\overrightarrow{a}$，$\overrightarrow{b}$是平面上的两个单位向量，$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{5}$．若m∈R，则|$\overrightarrow{a}$+m$\overrightarrow{b}$|的最小值是（　　）

A．

$\frac{3}{4}$

B．

$\frac{4}{3}$

C．

$\frac{4}{5}$

D．

$\frac{5}{4}$

10．设双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1（a＞0，b＞0）的离心率是3，则其渐近线的方程为（　　）

A．

$x±2\sqrt{2}y=0$

B．

$2\sqrt{2}x±y=0$

C．

x±8y=0

D．

8x±y=0

9．在平面直角坐标系中，不等式组$\left\{\begin{array}{l}3x-2y≥0\\ 3x-y-3≤0\\ y≥0\end{array}\right.$表示的平面区域的面积是（　　）

A．

1

B．

$\frac{3}{2}$

C．

2

D．

$\frac{5}{2}$

8．在复平面内，复数z对应的点是Z（1，-2），则复数z的共轭复数$\overline z$=（　　）

A．

1+2i

B．

1-2i

C．

2+i

D．

2-i

7．在平面直角坐标系xOy中，A，B两点的坐标分别为（-2，0），（2，0），动点P满足：直线PA与直线PB的斜率之积为$-\frac{3}{4}$．
（Ⅰ）求动点P的轨迹E的方程；
（Ⅱ）过点A作两条互相垂直的直线l₁，l₂分别交曲线E于M，N两点，设l₁的斜率为k（k＞0），△AMN的面积为S，求$\frac{S}{k}$的取值范围．

6．设i是虚数单位，复数$z=\frac{{2{i^3}}}{1-i}$，则复数z的共轭复数为（　　）

A．

-1+i

B．

-1-i

C．

1-i

D．

1+i