14．如图.椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的离心率为$e=\frac{{\sqrt{3}}}{2}$.顶点为A1.A2.B1.B2.且$\overrig——青夏教育精英家教网—

相关习题

0 239121 239129 239135 239139 239145 239147 239151 239157 239159 239165 239171 239175 239177 239181 239187 239189 239195 239199 239201 239205 239207 239211 239213 239215 239216 239217 239219 239220 239221 239223 239225 239229 239231 239235 239237 239241 239247 239249 239255 239259 239261 239265 239271 239277 239279 239285 239289 239291 239297 239301 239307 239315 266669

科目： 来源： 题型：解答题

14．

如图，椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$e=\frac{{\sqrt{3}}}{2}$，顶点为A₁、A₂、B₁、B₂，且$\overrightarrow{{A_1}{B_1}}•\overrightarrow{{A_1}{B_2}}=3$．
（1）求椭圆C的方程；
（2）P是椭圆C上除顶点外的任意点，直线B₂P交x轴于点Q，直线A₁B₂交A₂P于点E．设A₂P的斜率为k，EQ的斜率为m，试问2m-k是否为定值？并说明理由．

查看答案和解析>>

科目： 来源： 题型：解答题

13．

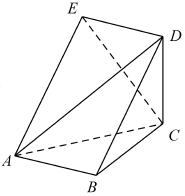如图，五面体ABCDE中，四边形ABDE是菱形，△ABC是边长为2的正三角形，∠DBA=60°，$CD=\sqrt{3}$．
（1）证明：DC⊥AB；
（2）若点C在平面ABDE内的射影H，求CH与平面BCD所成的角的正弦值．

查看答案和解析>>

科目： 来源： 题型：解答题

12．

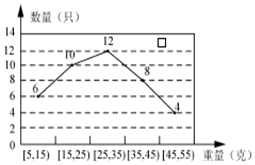某经销商从外地水产养殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如图：
（1）记事件A为：“从这批小龙虾中任取一只，重量不超过35g的小龙虾”，求P（A）的估计值；
（2）若购进这批小龙虾100千克，试估计这批小龙虾的数量；
（3）为适应市场需求，了解这批小龙虾的口感，该经销商将这40只小龙虾分成三个等级，如下表：

等级	一等品	二等品	三等品
重量（g）	[5，25）	[25，45）	[45，55]

按分层抽样抽取10只，再随机抽取3只品尝，记X为抽到二等品的数量，求抽到二级品的期望．

查看答案和解析>>

科目： 来源： 题型：解答题

11．已知函数f（x）=sinωxcosωx-$\sqrt{3}{cos^2}ωx+\frac{{\sqrt{3}}}{2}$（ω＞0）图象的两条相邻对称轴为$\frac{π}{2}$．
（1）求函数y=f（x）的对称轴方程；
（2）若函数y=f（x）-$\frac{1}{3}$在（0，π）上的零点为x₁，x₂，求cos（x₁-x₂）的值．

查看答案和解析>>

科目： 来源： 题型：填空题

10．

如图所示，由直线x=a，x=a+1（a＞0），y=x²及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间，即${a^2}＜\int_a^{a+1}{{x^2}dx＜{{（a+1）}^2}}$．类比之，若对?n∈N₊，不等式$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}＜1n4＜\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$恒成立，则实数k等于2．

查看答案和解析>>

科目： 来源： 题型：填空题

9．

某多面体的三视图如图所示，则该多面体外接球的体积为$\frac{{41\sqrt{41}}}{48}π$．