科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

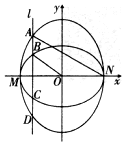16．如图，已知椭圆C₁的中心在原点O，长轴左、右端点M、N在x轴上，椭圆C₂的短轴为MN，且C₁、C₂的离心率都为e，直线l⊥MN，l与C₁交于两点，与C₂交于两点，这四点纵坐标从大到小依次为A、B、C、D．
（1）设$e=\frac{1}{2}$，求|BC|与|AD|的比值；
（2）若存在直线l，使得BO∥AN，求椭圆离心率e的取值范围．

科目： 来源： 题型：解答题

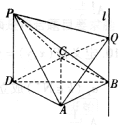15．四棱锥P-ABCD中，PD⊥面ABCD，底面ABCD是菱形，且PD=DA=2，∠CDA=60°，过点B作直线l∥PD，Q为直线l上一动点．
（1）求证：QP⊥AC；
（2）当二面角Q-AC-P的大小为120°时，求QB的长；
（3）在（2）的条件下，求三棱锥Q-ACP的体积．

科目： 来源： 题型：填空题

科目： 来源： 题型：选择题

13．一光源P在桌面A的正上方，半径为2的球与桌面相切，且PA与球相切，小球在光源P的中心投影下在桌面产生的投影为一椭圆，如图所示，形成一个空间几何体，且正视图是Rt△PAB，其中PA=6，则该椭圆的短轴长为（　　）

A．

6

B．

8

C．

$4\sqrt{3}$

D．

3

科目： 来源： 题型：选择题

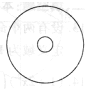12．如图，半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆，现将半径为1cm的一枚硬币抛到此纸板上，使整块硬币完全随机落在纸板内，则硬币与小圆无公共点的概率为（　　）

A．

$\frac{1}{2}$

B．

$\frac{21}{25}$

C．

$\frac{1}{4}$

D．

$\frac{3}{4}$

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

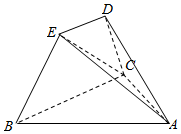10．如图所示，四棱锥A-BCDE，已知平面BCDE⊥平面ABC，BE⊥EC，DE∥BC，BC=2DE=6，AB=4$\sqrt{3}$，∠ABC=30°．
（1）求证：AC⊥BE；
（2）若∠BCE=45°，求三棱锥A-CDE的体积．

科目： 来源： 题型：解答题