12．已知函数f(x)=ex.g(x)=lnx+a．的最小值,与y=g(x)仅有一个交点P.证明:曲线y=f在点P处有相同的切线.且$a∈$．——青夏教育精英家教网—

相关习题

0 239296 239304 239310 239314 239320 239322 239326 239332 239334 239340 239346 239350 239352 239356 239362 239364 239370 239374 239376 239380 239382 239386 239388 239390 239391 239392 239394 239395 239396 239398 239400 239404 239406 239410 239412 239416 239422 239424 239430 239434 239436 239440 239446 239452 239454 239460 239464 239466 239472 239476 239482 239490 266669

科目： 来源： 题型：解答题

12．已知函数f（x）=e^x，g（x）=lnx+a．
（1）设h（x）=xf（x），求h（x）的最小值；
（2）若曲线y=f（x）与y=g（x）仅有一个交点P，证明：曲线y=f（x）与y=g（x）在点P处有相同的切线，且$a∈（{2，\frac{5}{2}}）$．

查看答案和解析>>

科目： 来源： 题型：解答题

11．已知椭圆Γ：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$经过点$M（{\sqrt{3}，\frac{1}{2}}）$，且离心率为$\frac{{\sqrt{3}}}{2}$．
（1）求椭圆Γ的方程；
（2）设点M在x轴上的射影为点N，过点N的直线l与椭圆Γ相交于A，B两点，且$\overrightarrow{NB}+3\overrightarrow{NA}$=0，求直线l的方程．

查看答案和解析>>

科目： 来源： 题型：解答题

10．

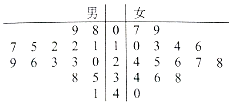某学校用简单随机抽样方法抽取了30名同学，对其每月平均课外阅读时间（单位：小时）进行调查，茎叶图如图：若将月均课外阅读时间不低于30小时的学生称为“读书迷”．
（1）将频率视为概率，估计该校900名学生中“读书迷”有多少人？
（2）从已抽取的7名“读书迷”中随机抽取男、女“读书迷”各1人，参加读书日宣传活动．
（i）共有多少种不同的抽取方法？
（ii）求抽取的男、女两位“读书迷”月均读书时间相差不超过2小时的概率．

查看答案和解析>>

科目： 来源： 题型：选择题

9．在平面直角坐标系xOy中，圆O的方程为x²+y²=4，直线l的方程为y=k（x+2），若在圆O上至少存在三点到直线l的距离为1，则实数k的取值范围是（　　）

A．

$[{0，\frac{{\sqrt{3}}}{3}}]$

B．

$[{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}]$

C．

$[{-\frac{1}{2}，\frac{1}{2}}]$

D．

$[{0，\frac{1}{2}}]$

查看答案和解析>>

科目： 来源： 题型：选择题

8．函数$f（x）=cos（{ωx+\frac{π}{6}}）$（ω＞0）的最小正周期为π，则f（x）满足（　　）

	A．	在$（{0，\frac{π}{3}}）$上单调递增		B．	图象关于直线$x=\frac{π}{6}$对称
	C．	$f（{\frac{π}{3}}）=\frac{{\sqrt{3}}}{2}$		D．	当$x=\frac{5π}{12}$时有最小值-1

查看答案和解析>>

科目： 来源： 题型：选择题

7．已知平面α⊥平面β，则“直线m⊥平面α”是“直线m∥平面β”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

查看答案和解析>>

科目： 来源： 题型：解答题

6．某学校用简单随机抽样方法抽取了100名同学，对其日均课外阅读时间（单位：分钟）进行调查，结果如下：

t	[0，15）	[15，30）	[30，45）	[45，60）	[60，75）	[75，90）
男同学人数	7	11	15	12	2	1
女同学人数	8	9	17	13	3	2

若将日均课外阅读时间不低于60分钟的学生称为“读书迷”．
（1）将频率视为概率，估计该校4000名学生中“读书迷”有多少人？
（2）从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动．
（i）求抽取的4位同学中既有男同学又有女同学的概率；
（ii）记抽取的“读书迷”中男生人数为X，求X的分布列和数学期望．

查看答案和解析>>

科目： 来源： 题型：填空题

5．数列{a_n}的前n项和为S_n，若S_n+a_n=4-$\frac{1}{{{2^{n-2}}}}（{n∈{N^*}}）$，则a_n=$\frac{n}{{2}^{n-1}}$．

查看答案和解析>>

科目： 来源： 题型：填空题

4．已知变量x，y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ 2x-y-1≤0\\ x+y-a≥0\end{array}\right.$，目标函数z=2x+y的最小值为-5，则实数a=-3．

查看答案和解析>>

科目： 来源： 题型：选择题

3．抛物线C：y²=4x的焦点为F，N为准线上一点，M为y轴上一点，∠MNF为直角，若线段MF的中点E在抛物线C上，则△MNF的面积为（　　）

A．

$\frac{{\sqrt{2}}}{2}$

B．