练习册

  • 练习册
  • 试题
    相关习题
     0  239298  239306  239312  239316  239322  239324  239328  239334  239336  239342  239348  239352  239354  239358  239364  239366  239372  239376  239378  239382  239384  239388  239390  239392  239393  239394  239396  239397  239398  239400  239402  239406  239408  239412  239414  239418  239424  239426  239432  239436  239438  239442  239448  239454  239456  239462  239466  239468  239474  239478  239484  239492  266669 

    科目： 来源： 题型：填空题

    12．某单位生产甲，乙，丙三种不同型号的产品，甲乙丙三种产品数量之比为3：4：5，现用分层抽样的方法抽出一个容量为96的样本，则乙种型号的产品数量为32．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．抛物线C：x2=2py（p＞0）的焦点为F，l为C的准线，P∈C．且|PF|=6，过P作l的垂线，垂足为M，若△FMP为正三角形，则p=（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目： 来源： 题型：选择题

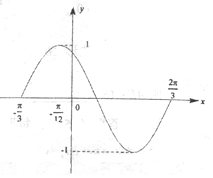    10．如图是函数y=Asin（ωx+φ）（x∈R）在区间[-$\frac{π}{3}$，$\frac{2π}{3}$]上的图象，为了得到这个函数的图象．只需将y=cosx（x∈R）的图象上的所有点（　　）
    A．向左平移$\frac{π}{6}$个单位长度，再把所有点的横坐标扩大到原来的2倍
    B．向左平移$\frac{π}{12}$个单位长度．再把所有点的横坐标扩大到原来的2倍
    C．把所有点的横坐标缩短到原来的$\frac{1}{2}$，再向左平移$\frac{π}{12}$个单位长度
    D．把所有点的横坐标缩短到原来的$\frac{1}{2}$，再向左平移$\frac{π}{6}$个单位长度

    查看答案和解析>>

    科目： 来源： 题型：选择题

    9．下列说法正确的是（　　）
    A．命题“?x0∈R，2${\;}^{{x}_{0}}$＞1”的否定是“?x∈R，2x≤1”
    B．命题“若x=y，则x2=y2”的否命题是“若x=y，则x2≠y2”
    C．p：?x∈R，x2+1≥1，q：在△ABC中，若sinA=$\frac{1}{2}$，则A=$\frac{π}{6}$，则p∧q为真命题
    D．若平面α⊥平面β，直线a?α，直线b?β，则a⊥b

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．方程ex=2-x的根位于（　　）
    A．（-1，0）B．（0，1）C．（1，2）D．（2，3）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    7．i是虚数单位，则$\frac{2i}{1+3i}$=（　　）
    A．-$\frac{3}{5}$+$\frac{1}{5}$iB．$\frac{3}{4}$-$\frac{1}{4}$iC．$\frac{3}{5}$+$\frac{1}{5}$iD．$\frac{3}{4}$+$\frac{1}{4}$i

    查看答案和解析>>

    科目： 来源： 题型：选择题

    6．已知函数f（x）=2cos（ωx+$\frac{3π}{2}$）（ω＞0），若存在m∈[$-\frac{2π}{3}$，0），n∈（0，$\frac{π}{4}$]，使得f（m）-f（n）=0．则实数ω的取值范围为（　　）
    A．（$\frac{5}{2}$，+∞）B．（$\frac{3}{4}$，+∞）C．（2，+∞）D．（$\frac{3}{2}$，+∞）

    查看答案和解析>>

    科目： 来源： 题型：解答题

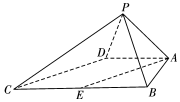    5．如图，四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是边长为2的等边三角形，E是BC的中点．
    （1）求证：AE∥平面PCD；
    （2）求四棱锥P-ABCD的体积．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    4．已知平面向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}$$|=1，\overrightarrow a$与$\overrightarrow b-\overrightarrow a$的夹角为60°，记$\overrightarrow m=λ\overrightarrow a+（{1-λ}）\overrightarrow b（{λ∈R}）$，则$|{\overrightarrow m}$|的取值范围为[$\frac{\sqrt{3}}{2}$，+∞）．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    3．若直线2x+y+m=0过圆x2+y2-2x+4y=0的圆心，则m的值为0．

    查看答案和解析>>

    同步练习册答案