
科目: 来源: 题型:选择题
| A. | $k≥\frac{3}{4}或k≤-4$ | B. | $k≥\frac{3}{4}或k≤-\frac{1}{4}$ | C. | -4≤k≤$\frac{3}{4}$ | D. | $\frac{3}{4}$≤k≤4 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{{3\sqrt{7}}}{7}$ | D. | $\frac{\sqrt{7}}{4}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 若l⊥m,m⊆α则l⊥α | B. | 若l∥α,m⊆α则l∥m | C. | 若l⊥α,l∥m则m⊥α | D. | 若l∥α,m∥α则l∥m |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
(1)用辗转相除法求228与1995的最大公约数.
(2)用秦九韶算法求多项式f(x)=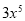 +
+ -8x+5在x=2时的值。
-8x+5在x=2时的值。
查看答案和解析>>
科目: 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
在对人们的休闲方式的一次调查中,共调查了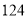 人,其中女性
人,其中女性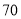 人,男性
人,男性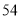 人.女性中有
人.女性中有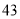 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有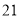 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动.
人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)是否有97.5%的把握认为性别与休闲方式有关系?
查看答案和解析>>
科目: 来源: 题型:解答题
| 时间 | (0,2) | [2,4) | [4,6) | [6,8) | 8小时以上 |
| 男生人数 | 10 | 25 | 35 | 30 | x |
| 女生人数 | 15 | 30 | 25 | y | 5 |
| 男生 | 女生 | 总计 | |
| 平均时间不超过6小时 | |||
| 平均时间超过6小时 | |||
| 总计 |
| K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ | P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 6.635 | 7.789 |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com