练习册

  • 练习册
  • 试题
    相关习题
     0  239493  239501  239507  239511  239517  239519  239523  239529  239531  239537  239543  239547  239549  239553  239559  239561  239567  239571  239573  239577  239579  239583  239585  239587  239588  239589  239591  239592  239593  239595  239597  239601  239603  239607  239609  239613  239619  239621  239627  239631  239633  239637  239643  239649  239651  239657  239661  239663  239669  239673  239679  239687  266669 

    科目： 来源： 题型：填空题

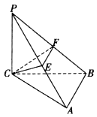    16．如图，已知在三棱锥P-ABC中，PC⊥平面ABC，AB⊥BC，若PC=BC=8，AB=4，E，F分别是PA，PB的中点，设三棱锥P-CEF的外接球的球心为O，则△AOB的面积为8$\sqrt{5}$．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．已知三棱锥S-ABC，△ABC是直角三角形，其斜边AB=8，SC⊥平面ABC，SC=6，则三棱锥的外接球的表面积为（　　）
    A．64πB．68πC．72πD．100π

    查看答案和解析>>

    科目： 来源： 题型：选择题

    14．中国古代儒家要求学生掌握六种基本才艺：礼、乐、射、御、书、数，简称“六艺”．某中学为弘扬“六艺”的传统文化，分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛．现有甲、乙、丙三位选手进入了前三名的最后角逐．规定：每场知识竞赛前三名的得分都分别为a，b，c（a＞b＞c，且a，b，c∈N*）；选手最后得分为各场得分之和．在六场比赛后，已知甲最后得分为26分，乙和丙最后得分都为11分，且乙在其中一场比赛中获得第一名，则下列说法正确的是（　　）
    A．每场比赛第一名得分a为4B．甲可能有一场比赛获得第二名
    C．乙有四场比赛获得第三名D．丙可能有一场比赛获得第一名

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．已知函数f（x）=|x+4|-|x-1|．
    （1）解不等式f（x）＞3；
    （2）若不等式f（x）+1≤4a-5×2a有解，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：选择题

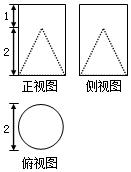    12．在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示，则此工艺部件的表面积为（　　）
    A．（7+$\sqrt{5}$）πB．（7+2$\sqrt{5}$）πC．（8+$\sqrt{5}$）πD．（8+2$\sqrt{5}$）π

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．已知在平面直角坐标系中，曲线f（x）=alnx+x在x=a处的切线过原点，则a=（　　）
    A．1B．eC．$\frac{1}{e}$D．0

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．一个几何体的三视图如图所示，则该几何体的体积为4$\sqrt{3}$+1．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．已知直线l的极坐标方程为ρsin（θ+$\frac{π}{4}$）=$\frac{{\sqrt{2}}}{2}$，圆C的参数方程为：$\left\{{\begin{array}{l}{x=2cosθ}\\{y=-2+2sinθ}\end{array}}\right.$（其中θ为参数）．
    （1）判断直线l与圆C的位置关系；
    （2）若椭圆的参数方程为$\left\{{\begin{array}{l}{x=2cosφ}\\{y=\sqrt{3}sinφ}\end{array}}\right.$（φ为参数），过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A，B两点，求|AB|．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．已知椭圆Γ：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率与双曲线x2-y2=a2的离心率之和为$\frac{3\sqrt{2}}{2}$，B1、B2为椭圆Γ短轴的两个端点，P是椭圆Γ上一动点（不与B1、B2重合），直线B1P、B2P分别交直线l：y=4于M、N两点，△B1B2P的面积记为S1，△PMN的面积记为S2，且S1的最大值为4$\sqrt{2}$．
    （1）求椭圆Γ的方程；
    （2）若S2=λS1，当λ取最小值时，求点P的坐标．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    7．富华中学的一个文学兴趣小组中，三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究，并且他们选择的名家各不相同．三位同学一起来找图书管理员刘老师，让刘老师猜猜他们三人各自的研究对象．刘老师猜了三句话：“①张博源研究的是莎士比亚；②刘雨恒研究的肯定不是曹雪芹；③高家铭自然不会研究莎士比亚．”很可惜，刘老师的这种猜法，只猜对了一句，据此可以推知张博源、高家铭和刘雨恒分别研究的是（　　）
    A．曹雪芹、莎士比亚、雨果B．雨果、莎士比亚、曹雪芹
    C．莎士比亚、雨果、曹雪芹D．曹雪芹、雨果、莎士比亚

    查看答案和解析>>

    同步练习册答案