已知中心在坐标原点O的椭圆C经过点A(32.4).点B(10.25)．(1)求椭圆C的方程,(2)已知圆M:x2+(y-5)2=9.双曲线G与椭圆C有相同的焦点.它的两条渐近线恰好与圆M相切.求双曲线——青夏教育精英家教网—

相关习题

0 23874 23882 23888 23892 23898 23900 23904 23910 23912 23918 23924 23928 23930 23934 23940 23942 23948 23952 23954 23958 23960 23964 23966 23968 23969 23970 23972 23973 23974 23976 23978 23982 23984 23988 23990 23994 24000 24002 24008 24012 24014 24018 24024 24030 24032 24038 24042 24044 24050 24054 24060 24068 266669

科目： 来源：不详 题型：解答题

已知中心在坐标原点O的椭圆C经过点A(3

，4)，点B(

，2

)．
（1）求椭圆C的方程；
（2）已知圆M：x²+（y-5）²=9，双曲线G与椭圆C有相同的焦点，它的两条渐近线恰好与圆M相切，求双曲线G的方程．

查看答案和解析>>

科目： 来源：不详 题型：填空题

椭圆的离心率等于

，且与双曲线

=1有相同的焦距，则椭圆的标准方程为______．

查看答案和解析>>

科目： 来源：不详 题型：单选题

已知a=4，b=1，焦点在x轴上的椭圆方程是（　　）

A．

+y2=1

B．x2+

C．

+y²=1

D．x2+

查看答案和解析>>

科目： 来源：不详 题型：单选题

若抛物线的准线方程为x=-7，则抛物线的标准方程为（　　）

A．x²=-28y

B．x²=28y

C．y²=-28x

D．y²=28x

查看答案和解析>>

科目： 来源：北京期末题 题型：解答题

已知椭圆

（a＞b＞0）的焦点分别是F₁（0，-1），F₂（0，1），且3a²=4b²，
（Ⅰ）求椭圆的方程；
（Ⅱ）设点P在这个椭圆上，且|PF₁|-|PF₂|=1，求∠F₁PF₂的余弦值。

查看答案和解析>>

科目： 来源：上海高考真题 题型：解答题

我们把由半椭圆

（x≥0）与半椭圆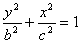

（x≤0）合成的曲线称作“果圆”，其中a²=
b²+c²，a＞0，b＞c＞0。
如图，设点F₀，F₁，F₂是相应椭圆的焦点，A₁，A₂和B₁，B₂是“果圆”与x，y轴的交点，M是线段A₁A₂的中点，
（1）若△F₀F₁F₂是边长为1的等边三角形，求该 “果圆”的方程；
（2）设P是“果圆”的半椭圆

（x≤0）上任意一点，求证：当|PM|取得最小值时，P在点
B₁，B₂或A₁处；
（3）若P是“果圆”上任意一点，求|PM|取得最小值时点P的横坐标。

查看答案和解析>>

科目： 来源： 题型：

（08年新建二中五模）如图,矩形与所在平面垂直,将矩形沿对折,使得翻折后点落在上,设.

⑴试求关于的函数解析式；

⑵当取最小值时,指出点的位置,并求出此时与平面所成的角；

⑶在条件⑵下,求三棱锥内切球的半径.

查看答案和解析>>

科目： 来源：不详 题型：解答题

在平面内，已知椭圆

=1(a＞b＞0)的两个焦点为F₁，F₂，椭圆的离心率为

，P点是椭圆上任意一点，且|PF₁|+|PF₂|=4，
（1）求椭圆的标准方程；
（2）以椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC，这样的等腰直角三角形是否存在？若存在请说明有几个、并求出直角边所在直线方程？若不存在，请说明理由．

查看答案和解析>>

科目： 来源：同步题 题型：单选题

已知两点M( -2 ，0) ，N(2 ，0) ，点P 满足

，则点P的轨迹方程为

[ ]

A．

B．x²+y²=16
C．y²-x²=8
D．x²+y²=8

查看答案和解析>>

科目： 来源：辽宁 题型：解答题

已知，椭圆C过点A(1，

)，两个焦点为（-1，0），（1，0）．
（1）求椭圆C的方程；
（2）E，F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学