
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
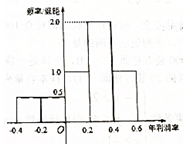 某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.
某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
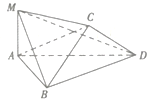 如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$
如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | $\sqrt{2}$sin1•f(1)>f($\frac{π}{4}$) | C. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | f(x)=3sin($\frac{π}{6}$-2x) | B. | f(x)=3sin(2x-$\frac{π}{6}$) | C. | f(x)=3sin($\frac{π}{3}$-2x) | D. | f(x)=3sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com