19．已知点P在圆C:x2+y2=4上.而Q为P在x轴上的投影.且点N满足$\overrightarrow{PN}=\overrightarrow{NQ}$.设动点N的轨迹为曲线E．(1)求曲线E的方——青夏教育精英家教网—

相关习题

0 239646 239654 239660 239664 239670 239672 239676 239682 239684 239690 239696 239700 239702 239706 239712 239714 239720 239724 239726 239730 239732 239736 239738 239740 239741 239742 239744 239745 239746 239748 239750 239754 239756 239760 239762 239766 239772 239774 239780 239784 239786 239790 239796 239802 239804 239810 239814 239816 239822 239826 239832 239840 266669

科目： 来源： 题型：解答题

19．已知点P在圆C：x²+y²=4上，而Q为P在x轴上的投影，且点N满足$\overrightarrow{PN}=\overrightarrow{NQ}$，设动点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）若A，B是曲线E上两点，且|AB|=2，O为坐标原点，求△AOB的面积的最大值．

查看答案和解析>>

科目： 来源： 题型：解答题

18．

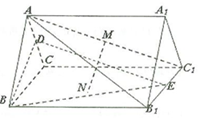如图，正三棱柱ABC-A₁B₁C₁中，侧棱$A{A_1}=\sqrt{3}$，AB=2，D，E分别为棱AC，B₁C₁的中点，M，N分别为线段AC₁和BE的中点．
（1）求证：直线MN∥平面ABC；
（2）求二面角C-BD-E的余弦值．

查看答案和解析>>

科目： 来源： 题型：解答题

17．

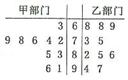渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩（单位：分）数据的茎叶图如图所示．
（1）若公司决定测试成绩高于85分的员工获得“职业技能好能手”称号，求从这20名员工中任选三人，其中恰有两人获得“职业技能好能手”的概率；
（2）公司结合这次测试成绩对员工的绩效奖金进行调整（绩效奖金方案如表），若以甲部门这10人的样本数据来估计该部门总体数据，且以频率估计概率，从甲部门所有员工中任选3名员工，记绩效奖金不小于3a的人数为ξ，求ξ的分布列及数学期望．

分数	[60，70）	[70，80）	[80，90）	[90，100]
奖金	a	2a	3a	4a

查看答案和解析>>

科目： 来源： 题型：选择题

16．设A是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的右顶点，F（c，0）是右焦点，若抛物线${y^2}=-\frac{{4{a^2}}}{c}x$的准线l上存在一点P，使∠APF=30°，则双曲线的离心率的范围是（　　）

A．

[2，+∞）

B．

（1，2]

C．

（1，3]

D．

[3，+∞）

查看答案和解析>>

科目： 来源： 题型：选择题

15．函数f（x）=（1-cos2x）cos²x，x∈R，设f（x）的最大值是A，最小正周期为T，则f（AT）的值等于（　　）

A．

$\frac{1}{4}$

B．

$\frac{1}{2}$

C．

D．

查看答案和解析>>

科目： 来源： 题型：选择题

14．等差数列{a_n}满足a₁=1，a₂+a₃=3，则a₁+a₂+a₃+a₄+a₅+a₆+a₇=（　　）

A．

B．

C．

D．

查看答案和解析>>

科目： 来源： 题型：选择题

13．已知集合A={x|x²+x-6＜0}，B={-2，-1，0，1，2}，那么A∩B=（　　）

A．

{-2，-1，0，1}

B．

{-2，-1，1}

C．

{-1，1，2}

D．

{-1，0，1，2}

查看答案和解析>>

科目： 来源： 题型：解答题

12．

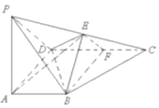如图，在四棱锥P-ABCD中，PA⊥面ABCD，AB∥CD，CD⊥AD，AD=CD=2AB=2，E，F分别为PC，CD的中点
（1）求证：平面ABE⊥平面BEF
（2）设PA=a，若平面EBD与平面ABCD所成锐二面角θ∈[$\frac{π}{4}$，$\frac{π}{3}$]，求a的取值范围．

查看答案和解析>>

科目： 来源： 题型：填空题

11．若m=${∫}_{-1}^{1}$（6x²+tanx）dx，且（2x+$\sqrt{3}$）^m=a₀+a₁x+a₂x²+…+a_mx^m，则（a₀+a₂+…+a_m）²-（a₁+..+a_m-1）²的值为1．

查看答案和解析>>

科目： 来源： 题型：填空题

10．设x，y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥\frac{1}{2}x}\\{2x+y≤10}\end{array}\right.$，向量$\overrightarrow{a}$=（y²+x²，m），$\overrightarrow{b}$=（1，1），且$\overrightarrow{a}∥\overrightarrow{b}$，则m的最小值为$\frac{5}{4}$．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学