
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
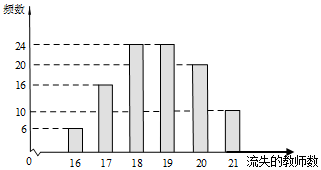 2017年两会继续关注了乡村教师的问题,随着城乡发展失衡,乡村教师待遇得不到保障,流失现象严重,教师短缺会严重影响乡村孩子的教育问题,为此,某市今年要为某所乡村中学招聘储备未来三年的教师,现在每招聘一名教师需要2万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要5万元,已知现在该乡村中学无多余教师,为决策应招聘多少乡村教师搜集并整理了该市100所乡村中学在过去三年内的教师流失数,得到右面的柱状图:记x表示一所乡村中学在过去三年内流失的教师数,y表示一所乡村中学未来四年内在招聘教师上所需的费用(单位:万元),n表示今年为该乡村中学招聘的教师数,为保障乡村孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘
2017年两会继续关注了乡村教师的问题,随着城乡发展失衡,乡村教师待遇得不到保障,流失现象严重,教师短缺会严重影响乡村孩子的教育问题,为此,某市今年要为某所乡村中学招聘储备未来三年的教师,现在每招聘一名教师需要2万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要5万元,已知现在该乡村中学无多余教师,为决策应招聘多少乡村教师搜集并整理了该市100所乡村中学在过去三年内的教师流失数,得到右面的柱状图:记x表示一所乡村中学在过去三年内流失的教师数,y表示一所乡村中学未来四年内在招聘教师上所需的费用(单位:万元),n表示今年为该乡村中学招聘的教师数,为保障乡村孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘查看答案和解析>>
科目: 来源: 题型:解答题
 如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.
如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
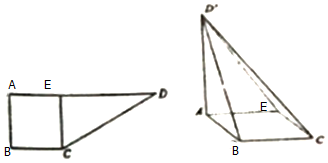
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{1}{11}$ | B. | $\frac{1}{12}$ | C. | $\frac{10}{11}$ | D. | $\frac{11}{12}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com