练习册

  • 练习册
  • 试题
    相关习题
     0  239751  239759  239765  239769  239775  239777  239781  239787  239789  239795  239801  239805  239807  239811  239817  239819  239825  239829  239831  239835  239837  239841  239843  239845  239846  239847  239849  239850  239851  239853  239855  239859  239861  239865  239867  239871  239877  239879  239885  239889  239891  239895  239901  239907  239909  239915  239919  239921  239927  239931  239937  239945  266669 

    科目： 来源： 题型：选择题

    4．已知直线l：y=2x+m与曲线y=-$\sqrt{4-{x}^{2}}$有两个公共点，则实数m的取值范围是（　　）
    A．[-2$\sqrt{5}$，-4]B．（-2$\sqrt{5}$，-4]C．[-2$\sqrt{5}$，-4）D．（-2$\sqrt{5}$，-4）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    3．设不等式|x-2|＜a的解集为A，且$\frac{3}{2}$∈A，$\frac{1}{2}$∉A，则a的取值范围是（　　）
    A．$\frac{1}{2}$＜a＜$\frac{3}{2}$B．$\frac{1}{2}$≤a＜$\frac{3}{2}$C．$\frac{1}{2}$＜a≤$\frac{3}{2}$D．$\frac{1}{2}$≤a≤$\frac{3}{2}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    2．已知空间几何体CBEADF如图所示，底面AEFD为矩形，平面BEFC⊥平面AEFD，∠CFE=∠BEF=90°，其中AE+BE=AD=2，DF+CF=4．
    （1）若AE=1，G为棱CF上靠近点F的三等分点，证明：DG∥平面ABC；
    （2）当VE-ABF=$\frac{1}{3}$时，求直线BF与CA所成角的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    1．已知函数f（x）=$\frac{alnx}{x}$+b（a，b∈R）的图象在点（1，f（1））处的切线方程为y=x-1．
    （1）求实数a，b的值及函数f（x）的单调区间．
    （2）当f（x1）=f（x2）（x1≠x2）时，比较x1+x2与2e（e为自然对数的底数）的大小．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    4．如图，四棱锥P-ABCD的底面ABCD是平行四边形，侧面PAD是边长为2的正三角形，AB=BD=$\sqrt{5}$，PB=$\sqrt{7}$
    （Ⅰ）求证：平面PAD⊥平面ABCD；
    （Ⅱ）设Q是棱PC上的点，当PA∥平面BDQ时，求QB与面ABCD成角的正弦值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

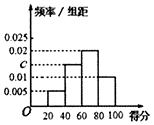    3．某校为了解校园安全教育系列活动的成效，对全校学生进行一次安全意识测试，根据测试成绩评定“合格”、“不合格”两个等级，同时对相应等级进行量化：“合格”记5分，“不合格”记为0分．现随机抽取部分学生的答卷，统计结果及对应的频率分布直方图如下所示．
    等级不合格合格
    得分[20，40）[40，60）[60，80）[80，100]
    频数6a24b
    （Ⅰ）求a，b，c的值；
    （Ⅱ）用分层抽样的方法，从评定等级为“合格”和“不合格”的学生中选取5人进行座谈．现再从这5人中任选2人，求这两人都合格的概率．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    2．定义在R上的奇函数f（x）满足f（x-2）=-f（x），且在[0，1]上是增函数，则f（$\frac{1}{4}$），f（-$\frac{1}{4}$），f（$\frac{3}{2}$）的大小关系是$f（-\frac{1}{4}）$＜$f（\frac{1}{4}）$＜$f（\frac{3}{2}）$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    1．在△ABC三个内角A，B，C所对的边分别为a，b，c，若c2sinA=5sinC，（a+c）2=16+b2，则△ABC的面积是2．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    20．在平面直角坐标系中，O为坐标原点，A（-1，2），B（3，4），C为AB中点，则$\overrightarrow{AB}$•$\overrightarrow{OC}$的值是（　　）
    A．10B．-10C．20D．-20

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．已知各项都为正数的数列{an}满足a1=1，an2-（2an-1-1）an-2an-1=0（n≥2，n∈N*），数列{bn}满足b1=1，b1+$\frac{1}{2}$b2+$\frac{1}{3}$b3+…+$\frac{1}{n}$bn=bn+1-1（n∈N*）
    （Ⅰ）求{an}，{bn}的通项公式；
    （Ⅱ）求数列{an•bn}的前n项和为Tn．

    查看答案和解析>>

    同步练习册答案