科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

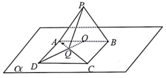12．如图，平面PAB⊥平面α，AB?α，且△PAB为正三角形，点D是平面α内的动点，ABCD是菱形，点O为AB中点，AC与OD交于点Q，I?α，且l⊥AB，则PQ与I所成角的正切值的最小值为（　　）

A．

$\sqrt{-3+\frac{3\sqrt{7}}{2}}$

B．

$\sqrt{3+\frac{3\sqrt{7}}{2}}$

C．

$\sqrt{7}$

D．

3

科目： 来源： 题型：解答题

11．在平面直角坐标系xOy中，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为e，D为右准线上一点．
（1）若e=$\frac{1}{2}$，点D的横坐标为4，求椭圆的方程；
（2）设斜率存在的直线l经过点P（$\frac{3a}{4}$，0），且与椭圆交于A，B两点．若$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OD}$，DP⊥l，求椭圆离心率e．

科目： 来源： 题型：选择题

10．“杨辉三角形”是古代重要的数学成就，它比西方的“帕斯卡三角形”早了300多年，如图是三角形数阵，记a_n为图中第n行各个数之和，则a₅+a₁₁的值为（　　）

A．

528

B．

1020

C．

1038

D．

1040

科目： 来源： 题型：解答题

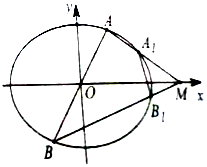9．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，焦距为2，直线y=kx（x≠0）与椭圆C交于A，B两点，M为其右准线与x轴的交点，直线AM，BM分别与椭圆C交于A₁，B₁两点，记直线A₁B₁的斜率为k₁
（1）求椭圆C的方程；
（2）是否存在常数λ，使得k₁=λk恒成立？若存在，求出λ的值；若不存在，请说明理由．

科目： 来源： 题型：填空题

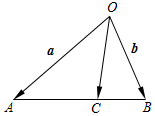8．如图，在△OAB中，C是AB上一点，且AC=2CB，设 $\overrightarrow{OA}=\overrightarrow a，\overrightarrow{OB}=\vec b$，则$\overrightarrow{OC}$=$\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$．（用$\overrightarrow a，\overrightarrow b$表示）

科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

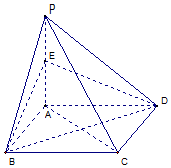6．如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，点E为PA的中点．
（1）求证：PC∥平面BED；
（2）求异面直线AD与PB所成角的大小．

科目： 来源： 题型：解答题