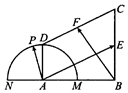17．在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的半圆分别交BA及其延长线于点M，N，点P在$\widehat{MDN}$上运动（如图）．若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$，其中λ，μ∈R，则2λ-5μ的取值范围是（　　）

A．

[-2，2]

B．

$[{-2，2\sqrt{2}}]$

C．

$[{-2\sqrt{2}，2}]$

D．

$[{-2\sqrt{2}，2\sqrt{2}}]$

16．在平面直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=m+\sqrt{2}t}\\{y=\sqrt{2}t}\end{array}\right.$ （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ²=$\frac{4}{1+si{n}^{2}θ}$，且直线l经过点F（-$\sqrt{2}$，0）
（ I ）求曲线C的直角坐标方程和直线l的普通方程；
（Ⅱ）设曲线C的内接矩形的周长为L，求L的最大值．

15．已知a＞0，函数f（x）=ln（x-1）-a（x-2），g（x）=e^x+（a²-2）x
（1）求f（x）在区间[2，3]上的最小值；
（2）设h（x）=af（x+2）+g（x），当x≥0时，h（x）≥-1恒成立，求实数的取值范围．

14．现从某班的一次期末考试中，随机的抽取了七位同学的数学（满分150分）、物理（满分110分）成绩如表所示，数学、物理成绩分别用特征量t，y表示，

特征量	1	2	3	4	5	6	7
t	101	124	119	106	122	118	115
y	74	83	87	75	85	87	83

（1）求y关于t的回归方程；
（2）利用（1）中的回归方程，分析数学成绩的变化对物理成绩的影响，并估计该班某学生数学成绩130分时，他的物理成绩（精确到个位）．
附：回归方程$\widehaty=\widehatbt+\widehata$中斜率和截距的最小二乘估计公式分别为：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$．${\sum_{i=1}^7{（{{t_i}-\overline t}）}^2}=432$．

13．齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马，现从双方的马匹中随机选一匹进行一场比赛，则在齐王的马获胜的条件下，齐王的上等马获胜的概率为（　　）

A．

$\frac{2}{3}$

B．

$\frac{1}{2}$

C．

$\frac{1}{3}$

D．

1

12．某三棱锥的三视图如图所示，已知该三棱锥的外接球的表面积为12π，则此三棱锥的体积为（　　）

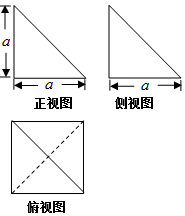
A．

4

B．

$\frac{4}{3}$

C．

$\frac{8}{3}$

D．

$\frac{1}{3}$

11．已知直线l的参数方程为$\left\{{\begin{array}{l}{x=-1-\frac{{\sqrt{3}}}{2}t}\\{y=\sqrt{3}+\frac{1}{2}t}\end{array}}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为$ρ=4sin（θ-\frac{π}{6}）$．
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设点为P（x，y）为直线l与圆C所截得的弦上的动点，求$\sqrt{3}x+y$的取值范围．

10．执行如图所示的程序框图，若输入n=5，则输出的S值为（　　）

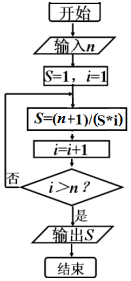
A．

$\frac{1}{20}$

B．

$\frac{5}{16}$

C．

$\frac{16}{5}$

D．

$\frac{3}{8}$

9．已知单位向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0，0≤x≤$\frac{1}{2}$≤y≤1，则|x$\overrightarrow{a}$+y$\overrightarrow{b}$+（1-x-y）$\overrightarrow{c}$|的最小值为$\frac{1}{4}$．

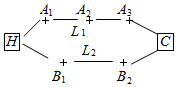8．如图，李先生家住H小区，他工作在C处科技园区，从家开车到公司上班路上有L₁、L₂两条路线，L₁路线上有A₁、A₂、A₃三个路口，各路口遇到红灯的概率均为$\frac{1}{2}$；L₂路线上有B₁、B₂两个路口，各路口遇到红灯的概率依次为$\frac{3}{4}$，$\frac{3}{5}$．
（1）若走L₂路线，求遇到红灯次数X的分布列和数学期望；
（2）按照“平均遇到红灯次数最少”的要求，请你帮助李先生从上述两条路线中选择一条最好的上班路线，并说明理由．