17．在极坐标系中，直线l和圆C的极坐标方程为ρcos（θ+$\frac{π}{6}$）=a（a∈R）和ρ=4sinθ．若直线l与圆C有且只有一个公共点，求a的值．

16．已知矩阵A=$[\begin{array}{l}{2}&{-2}\\{0}&{1}\end{array}]$，设曲线C：（x-y）²+y²=1在矩阵A对应的变换下得到曲线C′，求C′的方程．

15．已知函数f（x）=lnx+a（x²-3x+2），其中a为参数．
（1）当a=0时，求函数f（x）在x=1处的切线方程；
（2）讨论函数f（x）极值点的个数，并说明理由；
（3）若对任意x∈[1，+∞），f（x）≥0恒成立，求实数a的取值范围．

14．在区间（0，5）内任取一个实数m，则满足3＜m＜4的概率为$\frac{1}{5}$．

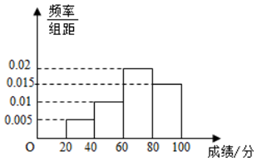13．随着社会的发展，食品安全问题渐渐成为社会关注的热点，为了提高学生的食品安全意识，某学校组织全校学生参加食品安全知识竞赛，成绩的频率分布直方图如图所示，数据的分组依次为[20，40），[40，60），[60，80），[80，100），若该校的学生总人数为3000，则成绩不超过60分的学生人数大约为900．

12．在平面直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}x=3cosα\\ y=\sqrt{3}sinα\end{array}\right.$（α为参数）．以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程为$ρcos（θ+\frac{π}{3}）=\sqrt{3}$．
（Ⅰ）求直线l的直角坐标方程和曲线C的普通方程；
（Ⅱ）设点P为曲线C上任意一点，求点P到直线l的距离的最大值．

11．某公司为了准确地把握市场，做好产品生产计划，对过去四年的数据进行整理得到了第x年与年销量y（单位：万件）之间的关系如表：

x	1	2	3	4
y	12	28	42	56

（Ⅰ）在图中画出表中数据的散点图；
（Ⅱ）根据（Ⅰ）中的散点图拟合y与x的回归模型，并用相关系数加以说明；
（Ⅲ）建立y关于x的回归方程，预测第5年的销售量约为多少？．
附注：参考数据：$\sqrt{\sum_{i=1}^4{{{（{y_i}-\overline y）}^2}}}≈32.6$，$\sqrt{5}≈2.24$，$\sum_{i=1}^4{{x_i}{y_i}=418}$．
参考公式：相关系数$r=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sqrt{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}\sum_{i=1}^n{{{（{y_i}-\overline y）}^2}}}}}$，
回归方程$\widehaty=\widehata+\widehatbx$中斜率和截距的最小二乘法估计公式分别为：$\widehatb=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．

10．设圆C满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3：1；③圆心到直线l：x-2y=0的距离为d．当d最小时，圆C的面积为2π．

9．若函数f（x）=2sinωx（0＜ω＜1）在区间$[{0，\frac{π}{3}}]$上的最大值为1，则ω=（　　）

A．

$\frac{1}{4}$

B．

$\frac{1}{3}$

C．

$\frac{1}{2}$

D．

$\frac{{\sqrt{3}}}{2}$

8．甲、乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完$\frac{2}{3}$局仍未出现连胜，则判定获胜局数多者赢得比赛．假设每局甲获胜的概率为$\frac{2}{3}$，乙获胜的概率为$\frac{1}{3}$，各局比赛结果相互独立．
（Ⅰ）求甲在4局以内（含 4 局）赢得比赛的概率；
（Ⅱ）记 X 为比赛决出胜负时的总局数，求X的分布列和数学期望．