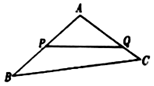
11．《九章算术》是我国古代内容极为丰富的数学名著，系统地总结了战国、秦、汉时期的数学成就．书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”，若某“阳马”的三视图如图所示（单位：cm），则该阳马的外接球的体积为（　　）

A．

100πcm3

B．

$\frac{500π}{3}c{m^3}$

C．

400πcm3

D．

$\frac{4000π}{3}c{m^3}$

10．一个三棱柱被一个平面截去一部分后，剩余部分的三视图如图所示，则该几何体的体积为（　　）

A．

10

B．

20

C．

30

D．

40

9．已知不等式|2x-3|+x-6≥0的解集为M．
（Ⅰ）求M；
（Ⅱ）当a，b∈M时，证明：$|\frac{a}{3}+\frac{3}{b}|≥|\frac{a}{b}+1|$．

8．在△ABC中，内角A，B，C的对边分别为a，b，c．已知$\sqrt{3}a=b（sinC+\sqrt{3}cosC）$．
（Ⅰ）求角B的大小；
（Ⅱ）若b=2，求a+c的取值范围．

7．如图，某生态园将一块三角形地ABC的一角APQ开辟为水果园，已知角A为120°，AB，AC的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆．
（1）若围墙AP、AQ总长度为200米，如何可使得三角形地块APQ面积最大？
（2）已知竹篱笆长为$50\sqrt{3}$米，AP段围墙高1米，AQ段围墙高2米，造价均为每平方米100元，求围墙总造价的取值范围．

6．已知数列{a_n}中，a₁=2，a_n+1=$\frac{2}{{a}_{n}+1}$，设b_n=$\frac{{a}_{n}-1}{{a}_{n}+2}$n∈N*
（1）求数列{b_n}的通项公式；
（2）设数列{b_n}的前n项的和为S_n，求证：b_nS_n≤$\frac{1}{16}$（n∈N*）

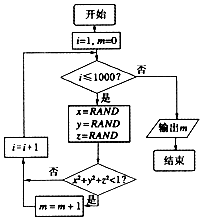5．我们可以用随机模拟的方法估计π的值，如图程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0，1）内的任何一个实数）．若输出的结果为527，则由此可估计π的近似值为（　　）

A．

3.126

B．

3.132

C．

3.151

D．

3.162

4．一个几何体的三视图如图所示，该几何体的表面积是$10+2\sqrt{5}$，则图中x的值为（　　）

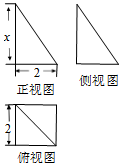
A．

$\sqrt{3}$

B．

$\sqrt{2}$

C．

2

D．

$\sqrt{5}$

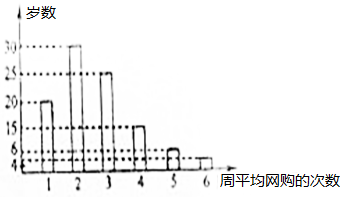3．网购是当前民众购物的新方式，某公司为改进营销方式，随机调查了100名市民，统计其周平均网购的次数，并整理得到如下的频数直方图．这10名市民中，年龄不超过40岁的有65人．将所抽样中周平均网购次数不小于4次的市民称为网购迷，且已知其中有5名市民的年龄超过40岁．
（1）根据已知条件完成下面的2×2列联表，能否在犯错的概率不超过0.10的前提条件下认为网购迷与年龄不超过40岁有关？
（2）现将所抽取样本中周平均网购次数不小于5次的市民称为超级网购迷，且已知超级网购迷中有2名年龄超过40岁，若从超级网购迷中任意挑选2名，求至少有1名市民年龄超过40岁的概率．
附：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$；

	网购迷	非网购迷	合计
年龄不超过40岁
年龄超过40岁
合计

2．我国古代数学名著《九章算术》的论割圆术中有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”它体现了一种无限与有限的转化过程．比如在表达式1+$\frac{1}{1+\frac{1}{1+…}}$中“…”即代表无数次重复，但原式却是个定值，它可以通过方程1+$\frac{1}{x}$=x求得x=$\frac{\sqrt{5}+1}{2}$．类比上述过程，则$\sqrt{3+2\sqrt{3+2\sqrt{…}}}$=（　　）

A．

3

B．

$\frac{\sqrt{13}+1}{2}$

C．

6

D．

2$\sqrt{2}$