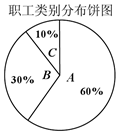15．某保险公司针对一个拥有20000人的企业推出一款意外险产品，每年每位职工只要交少量保费，发生意外后可一次性获得若干赔偿金．保险公司把企业的所有岗位共分为A、B、C三类工种，从事三类工种的人数分布比例如图，根据历史数据统计出三类工种的赔付频率如下表（并以此估计赔付频率）．

工种类别	A	B	C
赔付频率	$\frac{1}{1{0}^{5}}$	$\frac{2}{1{0}^{5}}$	$\frac{1}{1{0}^{4}}$

对于A、B、C三类工种职工每人每年保费分别为a元，a元，b元，出险后的赔偿金额分别为100万元，100万元，50万元，保险公司在开展此项业务过程中的固定支出为每年10万元．
（Ⅰ）若保险公司要求利润的期望不低于保费的20%，试确定保费a、b所要满足的条件；
（Ⅱ）现有如下两个方案供企业选择；
方案1：企业不与保险公司合作，企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工；
方案2：企业与保险公司合作，企业负责职工保费的60%，职工个人负责保费的40%，出险后赔偿金由保险公司赔付．
若企业选择方案2的支出（不包括职工支出）低于选择方案1的支出期望，求保费a、b所要满足的条件，并判断企业是否可与保险公司合作．（若企业选择方案2的支出低于选择方案1的支出期望，且与（Ⅰ）中保险公司所提条件不矛盾，则企业可与保险公司合作．）

14．如图所示，在三棱柱ABC-A₁B₁C₁中，AA₁B₁B为正方形，BB₁C₁C为菱形，B₁C⊥AC₁．
（Ⅰ）求证：平面AA₁B₁B⊥平面BB₁C₁C；
（Ⅱ）若D是CC₁中点，∠ADB是二面角A-CC₁-B的平面角，求直线AC₁与平面ABC所成角的余弦值．

13．规定：投掷飞镖3次为一轮，若3次中至少两次投中8环以上为优秀．根据以往经验某选手投掷一次命中8环以上的概率为$\frac{4}{5}$．现采用计算机做模拟实验来估计该选手获得优秀的概率：用计算机产生0到9之间的随机整数，用0，1表示该次投掷未在 8 环以上，用2，3，4，5，6，7，8，9表示该次投掷在 8 环以上，经随机模拟试验产生了如下 20 组随机数：
907  966  191  925  271  932  812  458  569  683
031  257  393  527  556  488  730  113  537  989
据此估计，该选手投掷 1 轮，可以拿到优秀的概率为（　　）

A．

$\frac{4}{5}$

B．

$\frac{18}{20}$

C．

$\frac{112}{125}$

D．

$\frac{17}{20}$

12．我国古代名著《九章算术》中有这样一段话：“今有金锤，长五尺，斩本一尺，重四斤．斩末一尺，重二斤．”意思是：“现有一根金锤，头部的1尺，重4斤；尾部的1尺，重2斤；且从头到尾，每一尺的重量构成等差数列．”则下列说法错误的是（　　）

	A．	该金锤中间一尺重3斤
	B．	中间三尺的重量和是头尾两尺重量和的3倍
	C．	该金锤的重量为15斤
	D．	该金锤相邻两尺的重量之差的绝对值为0.5斤

11．已知函数f（x）=|2x-1|+|x+1|．
（1）求函数f（x）的值域M；
（2）若a∈M，试比较|a-1|+|a+1|，$\frac{3}{2a}$，$\frac{7}{2}-2a$的大小．

10．已知函数f（x）=2mlnx-x，g（x）=$\frac{{3{e^x}-3}}{x^2}$（m∈R，e为自然对数的底数）．
（1）试讨论函数f（x）的极值情况；
（2）证明：当m＞1且x＞0时，总有g（x）+3f'（x）＞0．

9．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的长轴长为2$\sqrt{2}$，且椭圆C与圆M：（x-1）²+y²=$\frac{1}{2}$的公共弦长为$\sqrt{2}$．
（1）求椭圆C的方程．
（2）经过原点作直线l（不与坐标轴重合）交椭圆于A，B两点，AD⊥x轴于点D，点E在椭圆C上，且$（{\overrightarrow{AB}-\overrightarrow{EB}}）•（{\overrightarrow{DB}+\overrightarrow{AD}}）=0$，求证：B，D，E三点共线..

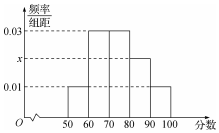8．2017高考特别强调了要增加对数学文化的考查，为此某校高三年级特命制了一套与数学文化有关的专题训练卷（文、理科试卷满分均为100分），并对整个高三年级的学生进行了测试．现从这些学生中随机抽取了50名学生的成绩，按照成绩为[50，60），[60，70），…，[90，100]分成了5组，制成了如图所示的频率分布直方图（假定每名学生的成绩均不低于50分）．
（1）求频率分布直方图中的x的值，并估计所抽取的50名学生成绩的平均数、中位数（同一组中的数据用该组区间的中点值代表）；
（2）若高三年级共有2000名学生，试估计高三学生中这次测试成绩不低于70分的人数；
（3）若在样本中，利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人，再从这6人中随机抽取3人参加这次考试的考后分析会，试求[80，90），[90，100]两组中至少有1人被抽到的概率．

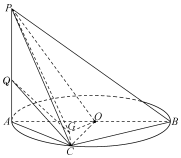7．如图，点C在以AB为直径的圆O上，PA垂直与圆O所在平面，G为△AOC的垂心．
（1）求证：平面OPG⊥平面PAC；
（2）若PA=AB=2AC=2，点Q在线段PA上，且PQ=2QA，求三棱锥P-QGC的体积．

6．已知函数f（x）=$\frac{1}{2}{x^2}$+mx（m＞0），数列{a_n}的前n项和为S_n，点（n，S_n）在f（x）图象上，且f（x）的最小值为-$\frac{1}{8}$．
（1）求数列{a_n}的通项公式；
（2）数列{b_n}满足b_n=$\frac{{{2^{a_n}}}}{{（{2^{a_n}}-1）（{2^{{a_{n+1}}}}-1）}}$，记数列{b_n}的前n项和为T_n，求证：T_n＜1．