3．在等差数列{a_n}中，已知a₂=-2，a₄=4，则公差等于（　　）

A．

1

B．

2

C．

3

D．

4

2．某几何体的三视图如图所示（单位：cm），则该几何体的表面积是38cm²，体积是12cm³．

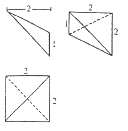1．已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体最长的棱长度为（　　）

A．

$2\sqrt{2}$

B．

$\sqrt{5}$

C．

3

D．

$2\sqrt{3}$

20．在△ABC中，$2\overrightarrow{BD}=\overrightarrow{DC}$，AB=4，AD=AC=3，则BC=$\sqrt{21}$．

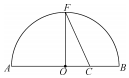19．《几何原本》卷2的几何代数法（以几何方法研究代数问题）成了后世西方数学家处理问题的重要依据，通过这一原理，很多的代数的公理或定理都能够通过图形实现证明，也称之为无字证明．现有如图所示图形，点F在半圆O上，点C在直径AB上，且OF⊥AB，设AC=a，BC=b，则该图形可以完成的无字证明为（　　）

	A．	$\frac{a+b}{2}≥\sqrt{ab}$（a＞0，b＞0）		B．	a2+b2≥2ab（a＞0，b＞0）
	C．	$\frac{2ab}{a+b}≤\sqrt{ab}$（a＞0，b＞0）		D．	$\frac{a+b}{2}≤\sqrt{\frac{{{a^2}+{b^2}}}{2}}$（a＞0，b＞0）

18．如图，已知正四棱柱（底面为正方形，侧棱与底面垂直）ABCD-A₁B₁C₁D₁的底面边长为3，侧棱长为4，连结A₁B，过A作AF⊥A₁B垂足为F，且AF的延长线交B₁B于E．
（Ⅰ）求证：AE⊥D₁B；
（Ⅱ）求三棱锥B-AEC的体积．

17．在一次数学测验后，班级学委王明对选答题的选题情况进行了统计，如下表：（单位：人）

	几何证明选讲	坐标系与参数方程	不等式选讲	合计
男同学	12	4	6	22
女同学	0	8	12	20
合计	12	12	18	42

（Ⅰ）在统计结果中，如果把《几何证明选讲》和《坐标系与参数方程》称为几何类，把《不等式选讲》称为代数类，我们可以得到如下2×2列联表：（单位：人）

	几何类	代数类	总计
男同学	16	6	22
女同学	8	12	20
总计	24	18	42

根据以下列联表，在犯错误不超过多少的情况下认为选做“几何类”或“代数类”与性别有关．
（Ⅱ）在原统计结果中，如果不考虑性别因素，按分层抽样的方法从选做不同选做题的同学中随机选出7名同学进行座谈．已知学委王明和两名数学科代表三人都在选做《不等式选讲》的同学中．
①求在这名班级学委被选中的条件下，两名数学科代表也被选中的概率；
②记抽到数学科代表的人数为X，求X的分布列及数学期望E（X）．
下面临界值表仅供参考：

P（K2≥k0）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k0	2.072	2.706	3.841	5.024	6.635	7.879	10.828

参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

16．已知定义在R上的奇函数f（x）满足f（x）=f（x+4）且f（3）=0，则方程f（x）=0在区间（0，10）内整数根有（　　）

A．

4个

B．

5个

C．

6个

D．

7个

15．对于某个给定的函数f（x），称方程f（x）=x的根为函数f（x）的不动点，若二次函数f（x）=ax²+bx+c（a＞0）有两个不动点x₁，x₂，且${x_2}-{x_1}＞\frac{1}{a}$，当t＜x₁时，f（t）与x₁的大小关系为（　　）

A．

f（t）＞x1

B．

f（t）≥x1

C．

f（t）＜x1

D．

f（t）≤x1

14．已知函数f（x）=（2x²-4ax）lnx+x²．
（1）设a＞0，求函数f（x）的单调区间．
（2）不等式（2x-4a）lnx＞-x对?x∈[1，+∞）恒成立，求a的取值范围．