练习册

  • 练习册
  • 试题
    相关习题
     0  239953  239961  239967  239971  239977  239979  239983  239989  239991  239997  240003  240007  240009  240013  240019  240021  240027  240031  240033  240037  240039  240043  240045  240047  240048  240049  240051  240052  240053  240055  240057  240061  240063  240067  240069  240073  240079  240081  240087  240091  240093  240097  240103  240109  240111  240117  240121  240123  240129  240133  240139  240147  266669 

    科目： 来源： 题型：选择题

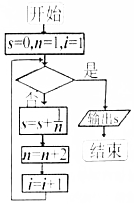
    13．如图所示给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图，其中判断框内应填入的条件是（　　）
    A．i＞1010B．i＜1010C．i＞1009D．i＜1009

    查看答案和解析>>

    科目： 来源： 题型：选择题

    12．复平面上平行四边形ABCD的四个顶点中，A、B、C所对应的复数分别为2-3i、-2-3i、-3+2i，则D点对应的复数是（　　）
    A．1+2iB．1-2iC．2-iD．2+i

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．已知函数f（x）=$\frac{lnx}{x}$．
    （1）求f（x）的最大值；
    （2）设a，b∈R，a＞b＞c（其中e是自然对数的底数），用分析法求证：ba＞ab．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．如图所示的三角形数阵叫“牛顿调和三角形”，它们是整数的倒数组成的，第n行有n个数且两端的数均为$\frac{1}{n}$（n≥2），每个数是它下一行左右相邻两数的和，如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$，$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$，$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$，…，则第6行第3个数（从左往右数）为$\frac{1}{60}$．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    9．已知定认在R上的可导函数f（x）的导函数f′（x），若对于任意实数x，有f′（x）＜f（x），且y=f（x）-1为奇函数，则不等式f（x）＜ex的解集为（　　）
    A．（0，+∞）B．（-∞，0）C．（-∞，e4）D．（e4，+∞）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．4个不同的小球全部随意放入3个不同的盒子里，使每个盒子都不空的放法种数为（　　）
    A．C${\;}_{4}^{1}$C${\;}_{4}^{3}$C${\;}_{2}^{2}$B．A${\;}_{3}^{1}$A${\;}_{4}^{3}$
    C．C${\;}_{4}^{3}$A${\;}_{2}^{2}$D．${C}_{4}^{2}{A}_{3}^{3}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    7．下面几种推理中是演绎推理的为（　　）
    A．科学家利用鱼的沉浮原理制造潜艇
    B．猜想数列$\frac{1}{1×2}$，$\frac{1}{2×3}$，$\frac{1}{3×4}$，…的通项公式为an=$\frac{1}{n（n+1）}$（n∈N+）
    C．半径为r的圆的面积S=πr2，则单位圆的面积S=π
    D．由平面直角坐标系中圆的方程为（x-a）2+（y-b）2=r2，推测空间直角坐标系中球的方程为（x-a）2+（y-b）2+（z-c）2=r2

    查看答案和解析>>

    科目： 来源： 题型：选择题

    6．下列求导运算正确的是（　　）
    A．（log2x）′=$\frac{1}{xln2}$B．（$\frac{cosx}{x}$）′=$\frac{xsinx-cosx}{x}$
    C．（10x）′=10xlgeD．（x+$\sqrt{x}$）′=1-$\frac{1}{2\sqrt{x}}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．（Ⅰ）计算由直线y=x-4，曲线y=$\sqrt{2x}$以及x轴所围图形的面积S．
    （Ⅱ）试判断$\sqrt{6}$+$\sqrt{7}$和2$\sqrt{2}$+$\sqrt{5}$的大小，并证明你的判断．

    查看答案和解析>>

    科目： 来源： 题型：解答题

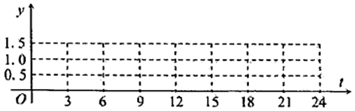
    4．已知某海滨浴场的海浪高度（单位：米）是时间（单位：小时，0≤t≤24）的函数，记作y=f（t），如表是某日各时的浪高数据：
     t（时） 03 6 9  1215  18 2124 
     y（米） 1.5 1.00.5  1.0 1.5 1.0 0.51.0 1.5 
    （Ⅰ）在如图的网格中描出所给的点；
    （Ⅱ）观察图，从y=at+b，y=at2+bt+c，y=Acos（ωx+p）中选择一个合适的函数模型，并求出该拟合模型的解析式；
    （Ⅲ）依据规定，当海浪高度高于1.25米时蔡对冲浪爱好者开放，请依据（Ⅱ）的结论判断一天内的8：00到20：00之间有多长时间可供冲浪爱好者进行活动．

    查看答案和解析>>

    同步练习册答案