练习册

  • 练习册
  • 试题
    相关习题
     0  241078  241086  241092  241096  241102  241104  241108  241114  241116  241122  241128  241132  241134  241138  241144  241146  241152  241156  241158  241162  241164  241168  241170  241172  241173  241174  241176  241177  241178  241180  241182  241186  241188  241192  241194  241198  241204  241206  241212  241216  241218  241222  241228  241234  241236  241242  241246  241248  241254  241258  241264  241272  266669 

    科目： 来源： 题型：选择题

    17．过点M（4，0）作圆x2+y2=4的两条切线MA，MB，A，B为切点，则$\overrightarrow{MA}$•$\overrightarrow{MB}$=（　　）
    A．6B．-6C．10D．6$\sqrt{3}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知函数f（x）=$\frac{1+cos2x}{\sqrt{2}sin（\frac{π}{2}+x）}$+$\sqrt{6}$sinx
    （Ⅰ）求函数y=f（x）的单调递增区间
    （Ⅱ）求函数y=f（x）在区间[0，$\frac{π}{2}$]上的最大值和最小值．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．在△ABC中，角A，B，C所对的边分别为a，b，c，若c2=（a+b）2-6，C=60°，则△ABC的面积是（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\sqrt{3}$C．$\frac{3\sqrt{3}}{2}$D．3$\sqrt{3}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    14．某公司8位员工的月工资（单位：元）为x1，x2，x3，…x8，其平均值和方差分别为$\overline{x}$和s2，若从下月起每位员工的月工资增加200元，则这8位员工下月工资的平均值和方差分别为（　　）
    A．$\overline{x}$，s2+2002B．$\overline{x}$+200，s2+2002C．$\overline{x}$+200，s2D．$\overline{x}$，s2

    查看答案和解析>>

    科目： 来源： 题型：解答题

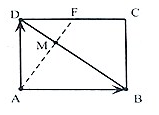    13．如图，在矩形ABCD中，F是边CD的中点，M是AF与BD交点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$
    （1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示向量$\overrightarrow{AF}$
    （2）证明：M是对角线BD的三等分点．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    12．给出下列说法：
    ①圆的渐开线的参数方程不能转化为普通方程；
    ②圆的渐开线也可以转化为普通方程，但是转化后的普通方程比较麻烦，且不容易看出坐标之间的关系，所以常使用参数方程研究圆的渐开线问题；
    ③在求圆的摆线和渐开线方程时，如果建立的坐标系原点和坐标轴选取不同，可能会得到不同的参数方程；
    ④圆的渐开线和x轴一定有交点而且是唯一的交点．
    其中正确的说法有（　　）
    A．①③B．②④C．②③D．①③④

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．关于渐开线和摆线的叙述，正确的是（　　）
    A．只有圆才有渐开线
    B．渐开线和摆线的定义是一样的，只是绘图的方法不一样，所以才得到了不同的图形
    C．正方形也可以有渐开线
    D．对于同一个圆，如果建立的直角坐标系的位置不同，画出的渐开线形状就不同

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．已知向量$\overrightarrow{AB}$=（1，-4），$\overrightarrow{BD}$=（2，1），$\overrightarrow{AD}$=（m，n），则m+n=0．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    9．圆心在原点，半径为2的圆的渐开线的参数方程是（　　）
    A．$\left\{\begin{array}{l}{x=2（cosφ+φsinφ）}\\{y=2（sinφ-φcosφ）}\end{array}\right.$（φ为参数）
    B．$\left\{\begin{array}{l}{x=4（cosθ+θsinθ）}\\{y=4（sinθ-θcosθ）}\end{array}\right.$（θ为参数）
    C．$\left\{\begin{array}{l}{x=2（φ-sinφ）}\\{y=2（1-cosφ）}\end{array}\right.$（φ为参数）
    D．$\left\{\begin{array}{l}{x=4（θ-sinθ）}\\{y=4（1-cosθ）}\end{array}\right.$（θ为参数）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，右顶点为A，上顶点为B，以坐标原点O为圆心，椭圆C的短轴长为直径作圆O，截直线AB的弦长为$\frac{6\sqrt{7}}{7}$（a2-b2）．
    （1）求椭圆C的标准方程；
    （2）是否存在过椭圆C的右焦点F的直线l，与椭圆C相交于G、H两点，使得△AFG与△AFH的面积比为1：2？若存在，求出直线l的方程；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案