练习册

  • 练习册
  • 试题
    相关习题
     0  241362  241370  241376  241380  241386  241388  241392  241398  241400  241406  241412  241416  241418  241422  241428  241430  241436  241440  241442  241446  241448  241452  241454  241456  241457  241458  241460  241461  241462  241464  241466  241470  241472  241476  241478  241482  241488  241490  241496  241500  241502  241506  241512  241518  241520  241526  241530  241532  241538  241542  241548  241556  266669 

    科目： 来源： 题型：填空题

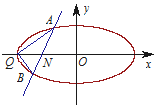    12．已知焦点在x轴上的椭圆C过点（0，1），且离心率为$\frac{{\sqrt{3}}}{2}$，Q为椭圆C的左顶点．
    （1）求椭圆C的标准方程；
    （2）已知过点$（-\frac{6}{5}，0）$的直线l与椭圆C交于A，B两点．
    ①若直线l垂直于x轴，求∠AQB的大小；
    ②若直线l与x轴不垂直，是否存在直线l使得△QAB为等腰三角形？如果存在，求出直线l的方程；如果不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    11．如图：在一个奥运场馆建设现场，现准备把一个半径为$\sqrt{3}$m的球形工件吊起平放到6m高的平台上，工地上有一个吊臂长DF=12m的吊车，吊车底座FG高1.5m．当物件与吊臂接触后，钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触．求物件能被吊车吊起的最大高度，并判断能否将该球形工件吊到平台上？

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．公差不为零的等差数列{an}的前n项之和为Sn，且${S_n}={（\frac{{{a_n}+k}}{2}）^2}$对n∈N*成立．
    （1）求常数k的值以及数列{an}的通项公式；
    （2）设数列{an}中的部分项${a_{k_1}}，{a_{k_2}}，{a_{k_3}}，…，{a_{k_n}}，…$，恰成等比数列，其中k1=2，k3=14，求kn．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    9．已知向量$\overrightarrow m=（sin（ωx+\frac{π}{3}），-1），\overrightarrow n=（\sqrt{3}，cos（ωx+\frac{π}{3}））（ω＞0）$，函数$f（x）=\overrightarrow m•\overrightarrow n$的图象的对称中心与对称轴之间的最小距离为$\frac{π}{4}$
    （1）求ω的值，并求函数f（x）在区间[0，π]上的单调增区间；
    （2）△ABC中，角A，B，C的对边分别为$a，b，c，f（A）=1，cosC=\frac{3}{5}，a=5\sqrt{3}$，求b的值．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    8．等差数列{an}各项均为正整数，满足：an+1＞an且a1a2-8a1+a2-13=0，数列{bn}满足${b_n}={n^2}（n∈{N^*}）$，数列{an}与{bn}所有公共项由小到大排列得到数列{cn}，数列{dn}满足${d_n}=\sum_{i=1}^n{\sqrt{1+\frac{1}{b_n}+\frac{1}{{{b_{n+1}}}}}}$，则4dn-c2n-1的最大值为2．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    7．平面直角坐标系xOy中，$A（-2，0），B（-\frac{1}{2}，0），P（{x_0}，{y_0}）$，满足：PA＜2PB，则直线x0x+y0y=1与圆x2+y2=1的公共点个数为2．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    6．在△ABC中，∠BAC=90°，BC=5，D，E为边BC上的两点，且满足：$\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC}，\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CB}$，则$\overrightarrow{AD}•\overrightarrow{AE}$的值为$\frac{50}{9}$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    5．已知$α∈（\frac{π}{2}，π）$且$cosα=-\frac{3}{5}$，则$tan（\frac{α}{2}-\frac{π}{4}）$=$\frac{1}{3}$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    4．已知函数f（x）=mlnx+nx，（m，n∈R），曲线y=f（x）在点（1，f（1））处的切线方程是x-2y-2=0，则m+n=$\frac{1}{2}$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    3．若从甲、乙、丙、丁4位同学中选出3名代表参加学校会议，则甲被选中的概率为$\frac{3}{4}$．

    查看答案和解析>>

    同步练习册答案