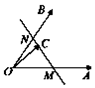2．如图所示，两个非共线向量$\overrightarrow{OA}$，$\overrightarrow{OB}$的夹角为θ，M、N分别为OA与OB的中点，点C在直线MN上，且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$（x，y∈R），则x²+y²的最小值为$\frac{1}{8}$．

1．在平面直角坐标系xoy中，以原点为极点，x轴的非负半轴为极轴建立极坐标系，直线l的参数方程为$\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\ y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数），曲线C的极坐标方程为ρ=6cosθ．
（Ⅰ）若直线l的参数方程中t=$\sqrt{2}$的时，得到M点，求M的极坐标方程和曲线C的直角坐标方程；
（Ⅱ）若点P（1，2），l和曲线C交于A，B两点，求$\frac{1}{|PA|}$+$\frac{1}{|PB|}$．

20．在极坐标系中，曲线C的方程为$ρ=4cosθ+2sinθ-\frac{3}{ρ}$，以极点O为原点，极轴为x轴的正半轴建立平面直角坐标系．
（Ⅰ）求曲线C的参数方程；
（Ⅱ）在直角坐标系中，点M（x，y）是曲线C上一动点，求x+y的最大值，并求此时点M的直角坐标．

19．根据“2015年国民经济和社会发展统计公报”中公布的数据，从2011 年到2015 年，我国的第三产业在GDP中的比重如下：

年份	2011	2012	2013	2014	2015
年份代码x	1	2	3	4	5
第三产业比重（%）	44.3	45.5	46.9	48.1	50.5

（Ⅰ）在所给坐标系中作出数据对应的散点图；
（Ⅱ）建立第三产业在GDP中的比重y关于年份代码x的回归方程；
（Ⅲ）按照当前的变化趋势，预测2017 年我国第三产业在GDP中的比重．
附注：回归直线方程$\widehaty=\widehata+\widehatbx$中的斜率和截距的最小二乘估计公式分别为：$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$\widehata=\overline y-\widehatb\overline x$，$\sum_{i=1}^5{{x_i}{y_i}}=720.9$．

18．已知曲线C：$\left\{\begin{array}{l}x=3cosθ\\ y=2sinθ\end{array}\right.$，直线l：ρ（cosθ-2sinθ）=12．
（1）将直线l的极坐标方程化为直角坐标方程，并写出曲线C的普通方程；
（2）设点P在曲线C上，求P点到直线l距离的最小值．

17．已知集合M={x∈N|x²-3x＜4}，N={x||x|＜2}，则M∩N=（　　）

A．

{x|-2≤x＜1}

B．

{x|-2＜x＜1}

C．

{0}

D．

{0，1}

16．已知斜率为2的直线的方程为5ax-5y-a+3=0，此直线在y轴上的截距为$\frac{1}{5}$．

15．要使圆x²+y²+Dx+Ey+F=0与x轴的两个交点分别位于原点的两侧，则有（　　）

	A．	D2+E2-4F＞0，且F＜0		B．	D＜0，F＞0
	C．	D≠0，F≠0		D．	F＜0

14．设F₁，F₂分别为椭圆${C_1}：\frac{x^2}{a_1^2}+\frac{y^2}{b_1^2}=1$（a₁＞b₁＞0）与双曲线${C_2}：\frac{x^2}{a_1^2}-\frac{y^2}{b_1^2}=1$（a₂＞b₂＞0）的公共焦点，它们在第一象限内交于点M，$∠{F_1}M{F_2}={90^0}$，若椭圆的离心率${e_1}∈[\frac{3}{4}，\frac{{2\sqrt{2}}}{3}]$，则双曲线C₂的离心率e₂的取值范围为$[\frac{{2\sqrt{14}}}{7}，\sqrt{2}）$．

13．命题p：|x-c|＜1，命题$q：\frac{4}{7-x}＞1$；若p是q的充分不必要条件，则实数c的取值范围为[4，6]．