
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题

查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 已知抛物线C1:x2=4y的焦点是椭圆C2短轴B1B2的一个端点B1,而双曲线C2:$\frac{{x}^{2}}{2}$-y2=1与椭圆C2共焦点.
已知抛物线C1:x2=4y的焦点是椭圆C2短轴B1B2的一个端点B1,而双曲线C2:$\frac{{x}^{2}}{2}$-y2=1与椭圆C2共焦点.查看答案和解析>>
科目: 来源: 题型:解答题
 如图所示的茎叶图记录了华润万家在渭南城区甲、乙连锁店四天内销售请客的某项指标统计:
如图所示的茎叶图记录了华润万家在渭南城区甲、乙连锁店四天内销售请客的某项指标统计:查看答案和解析>>
科目: 来源: 题型:解答题
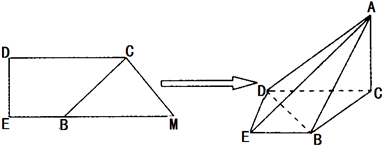
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com