9．以下三个命题中：
①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②老张身高176cm，他爷爷、父亲、儿子的身高分别是173cm、170cm和182cm，因儿子的身高与父亲的身高有关，用回归分析的方法得到的回归方程为$\widehaty=x+\widehata$，则预计老张的孙子的身高为180cm；
③若某项测量结果ξ服从正态分布N（1，σ²），且P（ξ≤4）=0.9，则P（ξ≤-2）=0.1．
其中真命题的个数为（　　）

A．

3

B．

2

C．

1

D．

0

8．已知数列{a_n}，{b_n}的各项均为正数，且对任意n∈N^*，都有b_n，a_n，b_n+1成等差数列．a_n，b_n+1，a_n+1成等比数列，且b₁=6，b₂=12．
（I）求证：数列$\left\{{\sqrt{a_n}}\right\}$是等差数列；
（Ⅱ）求．a_n，b_n．

7．口袋中有6个小球，其中4个红球，2个白球，从袋中任取2个小球．
（I）求所取2个小球都是红球的概率；
（Ⅱ）求所取2个小球颜色不相同的概率．

6．若$α∈（{\frac{π}{2}，π}），tanα=-\frac{1}{4}$，则sin（α+π）=-$\frac{\sqrt{17}}{17}$．

5．以下三个命题中，正确的个数是（　　）：
①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②老张身高176cm，他爷爷、父亲、儿子的身高分别是173cm、170cm和182cm，因儿子的身高与父亲的身高有关，用回归分析的方法得到的回归方程为$\widehaty=x+\widehata$，则预计老张的孙子的身高为180cm；
③设样本数据x₁，x₂，…，x₁₀的均值和方差均为2，若y_i=x_i+m（m为非零实数，i=1，2，…，10）的均值和方差分别为2+m，2．

A．

0

B．

1

C．

2

D．

3

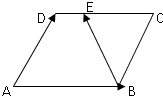4．在边长为1的菱形ABCD中，∠A=60°，E是线段CD上一点，满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|，如图所示，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$．
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{BE}$；
（2）在线段BC上是否存在一点F满足AF⊥BE？若存在，确定F点的位置，并求|$\overrightarrow{AF}$|；若不存在，请说明理由．

3．如图四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB∥CD，∠ABC=90°，且CD=2，AB=BC=PA=1，PD=$\sqrt{3}$．
（Ⅰ）求三棱锥A-PCD的体积；
（Ⅱ）问：棱PB上是否存在点E，使得PD∥平面ACE？若存在，求出$\frac{BE}{BP}$的值，并加以证明；若不存在，请说明理由．

2．已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在一个周期内的图象如图所示，其中M（$\frac{π}{12}$，2），N（$\frac{π}{3}$，0）．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）在△ABC中，角A，B，C的对边分别是a，b，c，且a=$\sqrt{13}$，c=3，f（$\frac{A}{2}$）=$\sqrt{3}$，求△ABC的面积．

1．某中学刚搬迁到新校区，学校考虑，若非住校生上学路上单程所需时间人均超过20分钟，则学校推迟5分钟上课．为此，校方随机抽取100个非住校生，调查其上学路上单程所需时间（单位：分钟），根据所得数据绘制成如下频率分布直方图，其中时间分组为[0，10），[10，20），[20，30），[30，40），[40，50]．
（Ⅰ）求频率分布直方图中a的值；
（Ⅱ）从统计学的角度说明学校是否需要推迟5分钟上课；
（Ⅲ）若从样本单程时间不小于30分钟的学生中，随机抽取2人，求恰有一个学生的单程时间落在[40，50]上的概率．

20．已知等比数列{a_n}的前n项和S_n=2ⁿ+r．
（Ⅰ）求实数r的值和{a_n}的通项公式；
（Ⅱ）若数列{b_n}满足b₁=1，b_n+1-b_n=log₂a_n+1，求b_n．