
科目: 来源:宁夏自治区期末题 题型:解答题
 (参数t∈R)与曲线C的极坐标方程为ρsin2θ=4cosθ.(1)求直线l与曲线C的普通方程;
(参数t∈R)与曲线C的极坐标方程为ρsin2θ=4cosθ.(1)求直线l与曲线C的普通方程; .
.查看答案和解析>>
科目: 来源:江苏同步题 题型:解答题
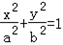 (a>b>0)的一个焦点
(a>b>0)的一个焦点 ,
,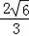 ).求抛物线C1及椭圆C2的方程.
).求抛物线C1及椭圆C2的方程.查看答案和解析>>
科目: 来源:期末题 题型:单选题
查看答案和解析>>
科目: 来源:月考题 题型:解答题
 ,且过原点存在两条互相垂直的直线与曲线y=(x)均相切,求y=f(x)
,且过原点存在两条互相垂直的直线与曲线y=(x)均相切,求y=f(x)查看答案和解析>>
科目: 来源:高考真题 题型:解答题
 ;求p的值及圆F的方程;
;求p的值及圆F的方程;查看答案和解析>>
科目: 来源:高考真题 题型:解答题
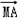 +
+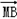 |=
|=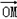 (
(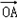 +
+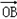 )+2。
)+2。查看答案和解析>>
科目: 来源:期末题 题型:解答题
 .
.查看答案和解析>>
科目: 来源:高考真题 题型:解答题
 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com