练习册

  • 练习册
  • 试题
    相关习题
     0  246178  246186  246192  246196  246202  246204  246208  246214  246216  246222  246228  246232  246234  246238  246244  246246  246252  246256  246258  246262  246264  246268  246270  246272  246273  246274  246276  246277  246278  246280  246282  246286  246288  246292  246294  246298  246304  246306  246312  246316  246318  246322  246328  246334  246336  246342  246346  246348  246354  246358  246364  246372  266669 

    科目： 来源： 题型：解答题

    13．某学校进行现代化达标验收，甲、乙、丙、丁四位评委随机去高三A、B两个班级听课，要求每个班级至少有一位评委且四位评委都要参与听课．
    （1）求评委甲去A班听课的概率；
    （2）设随机变量ξ是这四位评委去B班听课的人数，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    12．如图，一个靶子由四个同心圆组成，且半径分别为1，3，5，7，规定：击中A、B、C、D区域分别可获得5分、3分、2分、1分，脱靶（即击中最大圆之外的某点）得0分．甲射击时脱靶的概率为0.02，若未脱靶则等可能地击中靶子上的任意一点，求甲射击一次得分的数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．据统计某校学生在上学路上所需时间最多不超过120分钟，该校随机抽取部分新入校的学生就其上学路上所需时间（单位：分钟）进行调查，并将所得数据绘制成频率分布直方图．
    （1）为减轻学生负担，学校规定上学路上所需时间不少于1小时的学生可申请在校内住宿，请根据抽样数据估计该校600名新生中有多少学生可以申请在校内住宿．
    （2）从新入校的学生中任选4名学生，以频率分布直方图中的频率作为概率，这4名学生中上学所需时间少于20分钟的人数记为X，求X的分布列和期望．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．函数y=x3-3x的极小值是-2．

    查看答案和解析>>

    科目： 来源： 题型：解答题

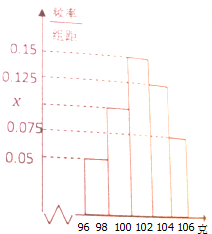    9．某工厂从一批产品中随机抽取40件进行检测，如图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106）．
    （1）求图中x的值；
    （2）若将频率视为概率，从这批产品中有放回的随机抽取3件，求至少有2件产品的净重在[98，100）中的概率；
    （3）若产品净重在[98，104）为合格产品，其余为不合格产品，从这40件抽样产品中任取2件，记ξ表示选到不合格产品的件数，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    8．在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F
    ①四边形BFD′E一定是平行四边形
    ②四边形BFD′E有可能是正方形
    ③四边形BFD′E在底面ABCD内的投影一定是正方形
    ④四边形BFD′E有可能垂直于平面BB′D′D
    以上结论正确的为①③④（写出所有正确结论的编号）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    7．某大学的一个社会实践调查小组，在对大学生的良好“光盘习惯”的调查中，随机发放了120份问卷，对回收的100份有效问卷进行统计，得到如下2×2列联表：
    做不到光盘能做到光盘合计
    男451055
    女301545
    合计7025100
    （1）现已按是否做到关盘分层从45份女生问卷中抽取了9份问卷，若从这9份问卷中随机抽取4份，并记其中能做到光盘的问卷的分数为ξ，试求随机变量ξ的分布列和数学期望；
    （2）如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P，那么，根据临界值表，最精确的P的值应为多少？请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．随着有车族人数的增加，越来越多的人都在关注汽油价格的信息，某机构调查市民获取有关汽车价格的信息渠道得到如下数据，按照信息来里利用分成抽样的方法抽取50人，其中获取信息的渠道为看电视的有27人．
    获取消息渠道看电视收听广播其它渠道
    男性480m180
    女性38421090
    （Ⅰ）求m的值；
    （Ⅱ）从“其它渠道”中按性别比例抽取一个容量为6的样本，再从这6人中抽取3人，求抽取的3人中至少1人是女性的概率；
    （Ⅲ）现从（Ⅱ）中确定的样本中每次都抽取1人，直到抽出所有女性为止，设所要抽取的人为X，求X的分布列和期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．一个不透明的盒子中关有蝴蝶、蜜蜂和蜻蜓三种昆虫共11只，现在盒子上开一小孔，每次只能一只昆虫飞出（假设任意一只昆虫等可能地飞出）已知若有2只昆虫先后任意飞出，飞出的是蝴蝶或蜻蜓的概率是$\frac{21}{55}$
    （1）求盒子中蜜蜂的数量
    （2）从盒子中先后任意飞出3只昆虫，记飞出蜜蜂的只数为X，求随机变量X的分布列与数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    4．已知函数f（x）=log4（4x+1）-（k-1）x（x∈R）为偶函数．
    （1）求常数k的值，并指出当x取何值时函数f（x）的值最小？并求出f（x）的最小值；
    （2）设g（x）=log4（a•2x-$\frac{4}{3}$a）（a≠0），且函数f（x）与g（x）的图象有公共点，求实数a的取值范围
    （3）指出实数a不同取值时，（2）中函数图象交点的个数．

    查看答案和解析>>

    同步练习册答案