
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 以上说法都不正确 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
 某中学为了解高三学生数学课程的学习情况,从全部2000名学生的数学考试成绩中随机抽取部分学生的考试成绩进行统计分析,得到如下的样本的频率分布直方图,已知成绩在[80,90)的学生共有40人,则样本中成绩在[60,80)内的人数为( )
某中学为了解高三学生数学课程的学习情况,从全部2000名学生的数学考试成绩中随机抽取部分学生的考试成绩进行统计分析,得到如下的样本的频率分布直方图,已知成绩在[80,90)的学生共有40人,则样本中成绩在[60,80)内的人数为( )| A. | 102 | B. | 104 | C. | 112 | D. | 114 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | a-b<c | B. | a<b-c | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目: 来源: 题型:解答题
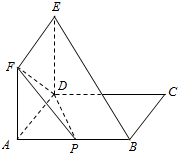 如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.
如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com