
科目: 来源: 题型:选择题
| A. | {$\sqrt{2}$} | B. | {2} | C. | {-$\sqrt{2}$,1,$\sqrt{2}$,2} | D. | {-2,1,$\sqrt{2}$,2} |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
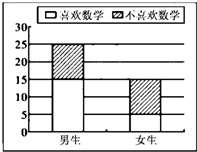 对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.
对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:选择题
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 95% | B. | 99% | C. | 97.5% | D. | 90% |
查看答案和解析>>
科目: 来源: 题型:解答题
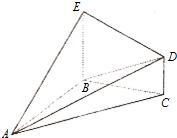
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com