练习册

  • 练习册
  • 试题
    相关习题
     0  246710  246718  246724  246728  246734  246736  246740  246746  246748  246754  246760  246764  246766  246770  246776  246778  246784  246788  246790  246794  246796  246800  246802  246804  246805  246806  246808  246809  246810  246812  246814  246818  246820  246824  246826  246830  246836  246838  246844  246848  246850  246854  246860  246866  246868  246874  246878  246880  246886  246890  246896  246904  266669 

    科目： 来源： 题型：填空题

    17．设全集U=R，集合A={x|x2-4x-5=0}，B={x|x2=1}，则A∩B={-1}，A∪B={-1，1，5}，A∩（∁UB）={5}．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    16．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=1，记|$\overrightarrow{c}$|的最大值为M，最小值为m，则M+m=（　　）
    A．2$\sqrt{3}$B．2C．$\sqrt{3}$D．1

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．已知a，b是实数，则“a＞|b|”是“a2＞b2”的（　　）
    A．充分必要条件B．充分不必要条件
    C．必要不充分条件D．既不充分也不必要条件

    查看答案和解析>>

    科目： 来源： 题型：选择题

    14．已知命题P：?x0∈R，x02+2x0+2≤0，则￢p是（　　）
    A．?x0∈R，x02+2x0+2＞0B．?x∈R，x2+2x+2≤0
    C．?x∈R，x2+2x+2＞0D．?x∈R，x2+2x+2≥0

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．设抛物线C1：y2=4x的焦点为F，动点D到点F的距离与到直线x=4的距离之比为$\frac{1}{2}$．
    （1）求动点D的轨迹C2的方程；
    （2）过点F作直线l与曲线C2交于P、Q两点，A1，A2为C2与x轴的交点，直线PA1，QA2相交于点M，直线PA2，QA1相交于点N，求证：MF⊥NF．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    12．不等式|x-2|+|x+3|≥7的解集是（-∞，-4]∪[3，+∞）．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的长轴长是（　　）
    A．2B．3C．4D．6

    查看答案和解析>>

    科目： 来源： 题型：解答题

    10．已知函数f（x）=ln（2ax+1）+$\frac{{x}^{3}}{3}$-x2-2ax（a∈R）．
    （1）若a=0，判断f（x）的单调性．
    （2）若y=f（x）在[4，+∞）上为增函数，求实数a的取值范围；
    （3）当a=-$\frac{1}{2}$时，方程f（1-x）=$\frac{（1-x）^{3}}{3}$+$\frac{b}{x}$有实根，求实数b的最大值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

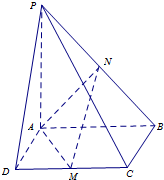    9．如图4，已知四棱锥P-ABCD，底面ABCD是正方形，PA⊥面ABCD，点M是CD的中点，点N是PB的中点，连接AM，AN，MN．
    （1）若PA=AB，求证：AN⊥平面PBC．
    （2）若MN=5，AD=3，求二面角N-AM-B的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

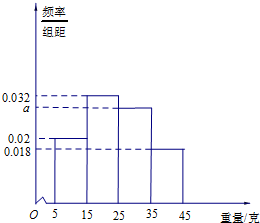    8．测量马口鱼性成熟时重量，从大量马口鱼中随机抽取100尾作为样本，测出它们的重量（单位：克），重量分组区间为（5，15]，（15，25]，（25，35]，（35，45]，由此得到重量样本的频率分布直方图，如图．
    （1）求a的值；
    （2）若重量在（25，35]，（35，45]中采用分层抽样方法抽出8尾作为特别实验，那么在（35，45]中需取出几尾？
    （3）从大量马口鱼中机抽取3尾，其中重量在（5，15]内的尾数为ξ，求ξ的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案