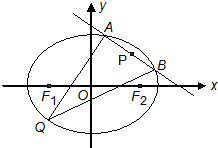11．如图所示，已知椭圆C的方程为$\frac{x^2}{2}+{y^2}$=1，F₁，F₂分别是椭圆C的左、右焦点，直线AB：y=kx+m（k＜0）与椭圆C交于不同的A，B两点．
（Ⅰ） 若k=-1，m=$\sqrt{2}$，点P在直线AB上求|PF₁|+|PF₂|的最小值；
（Ⅱ） 若以线段AB为直径的圆经过点F₂，且原点O到直线AB的距离为$\frac{{2\sqrt{5}}}{5}$．
（1）求直线AB的方程；
（2）在椭圆C上求点Q的坐标，使得△ABQ的面积最大．

10．已知数列{a_n}的前n项和为S_n，且S_n+a_n=4，n∈N^*
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）已知b_n=2n-17（n∈N^*），记c_n=log₂a_n-b_n．求数列{c_n}的前n项和T_n的最大值．

9．已知区域D：$\left\{\begin{array}{l}y≥2\\ x+y-2≥0\\ x-y-1≤0.\end{array}\right.$若圆C：（x-a）²+（y-2）²=2与区域D有公共点，则实数a的取值范围是（　　）

A．

[-1，5]

B．

[-2，2]

C．

[-2，5]

D．

[-1，2]

8．在给出如下三个命题：①若“p且q”为假命题，则p、q均为假命题；②命题“若a＞b，则2^a＞2^b-1”的否命题为“若a≤b，则2^a≤2^b-1”；下列判断正确的是（　　）

A．

假  真

B．

假  假

C．

真  假

D．

真  真

7．设i是虚数单位，若z=cosθ+isinθ且对应的点位于复平面的第二象限，则θ位于（　　）

A．

第一象限

B．

第二象限

C．

第三象限

D．

第四象限

6．设全集U是实数集R，M={x|x＞2或x＜-2}，N={x|x≥3或x＜1}，则（∁_UM）∩N是（　　）

A．

{x|-2≤x＜1}

B．

{x|-2≤x≤2}

C．

{x|1＜x≤2}

D．

{x|x＜2}

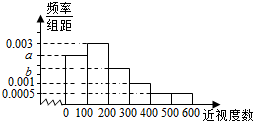5．某普通高中为了了解学生的视力状况，随机抽查了100名高二年级学生和100名高三年级学生，对这些学生配戴眼镜的度数（简称：近视度数）进行统计，得到高二学生的频数分布表和高三学生频率分布直方图如下：

近视度数	0-100	100-200	200-300	300-400	400以上
学生频数	30	40	20	10	0

将近视程度由低到高分为4个等级：当近视度数在0-100时，称为不近视，记作0；当近视度数在100-200时，称为轻度近视，记作1；当近视度数在200-400时，称为中度近视，记作2；当近视度数在400以上时，称为高度近视，记作3．
（Ⅰ）从该校任选1名高二学生，估计该生近视程度未达到中度及以上的概率；
（Ⅱ）设a=0.0024，从该校任选1名高三学生，估计该生近视程度达到中度或中度以上的概率；
（Ⅲ）把频率近似地看成概率，用随机变量X，Y分别表示高二、高三年级学生的近视程度，若EX=EY，求b．

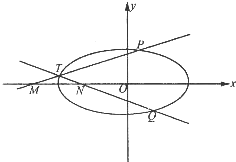4．如图所示，椭圆C的离心率为$\frac{\sqrt{3}}{2}$，以坐标原点O为圆心，椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切．
（1）求椭圆C的方程；
（2）设P，Q，T为椭圆C上不同的三点，且P，Q两点关于x轴对称，若直线PT，QT分别与x轴交于点M．N．求证：|OM|•|ON|为定值．

3．在直角坐标平面内，已知点A（1，0），B（-1，0），动点P满足|PA|+|PB|=4．
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ）过点（$\frac{1}{2}$，0）作直线l与轨迹C交于E、F两点，线段EF的中点为M，轨迹C与x轴正半轴的交点为N，求直线MN的斜率k的取值范围．

2．已知直线l：x=-2，圆C：x²+y²=4，动圆P恒与l相切，动圆P与圆C相交于A、B两点，且AB恒为圆C的直径，动圆P圆心的轨迹构成曲线E．
（Ⅰ）求曲线E的方程；
（Ⅱ）已知Q（-1，0）、F（1，0），过Q的直线m与曲线E交于M、N两点，设直线FM，FN的倾斜角分别为θ₁、θ₂，问θ₁+θ₂是否为定值，如果是定值，求出该定值，如果不是，请说明理由．