练习册

  • 练习册
  • 试题
    相关习题
     0  25778  25786  25792  25796  25802  25804  25808  25814  25816  25822  25828  25832  25834  25838  25844  25846  25852  25856  25858  25862  25864  25868  25870  25872  25873  25874  25876  25877  25878  25880  25882  25886  25888  25892  25894  25898  25904  25906  25912  25916  25918  25922  25928  25934  25936  25942  25946  25948  25954  25958  25964  25972  266669 

    科目： 来源：广东省模拟题 题型：解答题

    甲乙二人用4张扑克牌（分别是红桃2，红桃3，红桃4，方片4）玩游戏，他们将扑克牌洗匀后，背面朝上放在桌面上，甲先抽，乙后抽，抽出的牌不放回，各抽一张。
    （Ⅰ）设（i，j）表示甲乙抽到的牌的数字，（如甲抽到红桃2，乙抽到红桃3，记为（2，3）），请写出甲乙二人抽到的牌的所有情况；
    （Ⅱ）若甲抽到红桃3，则乙抽出的牌面数字比3大的概率是多少？
    （Ⅲ）甲乙约定，若甲抽到的牌的牌面数字比乙大，则甲胜；否则，乙胜，你认为此游戏是否公平？请说明理由。

    查看答案和解析>>

    科目： 来源：广东省模拟题 题型：解答题

    调查某初中1000名学生的肥胖情况，得下表：
     
    偏瘦
    正常
    肥胖
    女生（人）
    100
    173
    y
    男生（人）
    x
    177
    z
    已知从这批学生中随机抽取1名学生，抽到偏瘦男生的概率为0.15。
    （Ⅰ）求x的值；
    （Ⅱ）若用分层抽样的方法，从这批学生中随机抽取50名，问应在肥胖学生中抽多少名？
    （Ⅲ）已知y≥193，z≥193，肥胖学生中男生不少于女生的概率。

    查看答案和解析>>

    科目： 来源：广东省模拟题 题型：单选题

    从甲、乙、丙三人中任选两名代表，甲被选中的概率是
    [     ]
    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目： 来源：浙江省期末题 题型：单选题

    一个盒子里装有标号为1， 2， 3， 4， 5的5张标签，无放回的随机选取两张标签，则两张标签上的数字为相邻整数的概率是
    [     ]
    A、
    B、
    C、　
    D、

    查看答案和解析>>

    科目： 来源：北京期中题 题型：解答题

    某商场为吸引顾客消费推出一项优惠活动活动规则如下：消费额每 满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任…位置．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券，例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和。
    (1)若某位顾客消费128元，求返券金额不低于30元的概率；
    (2)若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X（元），求随机变量x的分布列和数学期望．

    查看答案和解析>>

    科目： 来源：北京期末题 题型：解答题

    为保护水资源，宣传节约用水，某校4名志愿者准备去附近的甲、乙、 丙三家公园进行宣传活动，每名志愿者都可以从三家公园中随机选择一家，且每人的选择相互独立。
    (Ⅰ)求4人恰好选择了同一家公园的概率；
    (Ⅱ)设选择甲公园的志愿者的人数为x，试求x的分布列及期望。

    查看答案和解析>>

    科目： 来源：北京模拟题 题型：解答题

    袋中装着标有数字l，2，3，4的小球各3个，从袋中任取3个小球，每个小球被取出的可能性都相等．
    (Ⅰ)求取出的3个小球上的数字互不相同的概率；
    (Ⅱ)用x表示取出的3个小球上所标的最大数字，求随机变量X的分布列和均值．

    查看答案和解析>>

    科目： 来源：广东省模拟题 题型：解答题

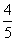    一射击运动员进行飞碟射击训练，每一次射击命中飞碟的概率p与运动员离飞碟的距离s（米）成反比，每一个飞碟飞出后离运动员的距离s（米）与飞行时问t（秒）满足s=15（t+1）(0≤t≤4)，每个飞碟允许该运动员射击两次（若第一次射击命中，则不再进行第二次射击）。该运动员在每一个飞碟飞出0.5秒时进行第一次射击，命中的概率为，当第一次射击没有命中飞碟，则在第一次射击后0.5秒进行第一次射击，子弹的飞行时间忽略小计．
    (Ⅰ)在第一个飞碟的射击训练时，若该运动员第一次射击没有命中，求他第二次射击命中飞碟的概率；
    (Ⅱ)求第一个飞碟被该运动员命中的概率；
    (Ⅲ)若该运动员进行三个飞碟的射击训练（每个飞碟是否被命中互不影响），求他至少命中两个飞碟的概率．

    查看答案和解析>>

    科目： 来源：山东省模拟题 题型：填空题

    五对夫妻排成一列，则每位丈夫总是排在他妻子的后面（可以不相邻）的概率为（    ）。

    查看答案和解析>>

    科目： 来源：天津模拟题 题型：解答题

    某地区举办青少年科技创新大赛，有50件科技创新作品进入了最后的评审阶段，大赛组委会对这50件作品分别从“艺术与创新”和“功能与实用”两项进行评分，每项评分均按等级采用5分制，若设“艺术与创新”得分为x，“功能与实用”得分为y，统计结果如下表：
    (Ⅰ)求“艺术与创新为4分且功能与实用为3分”的概率；
    (Ⅱ)若“功能与实用”得分的数学期望为，求a，b的值。

    查看答案和解析>>

    同步练习册答案