
科目: 来源:山东省高考真题 题型:解答题
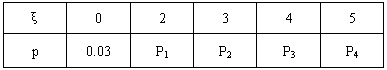
查看答案和解析>>
科目: 来源:湖南省高考真题 题型:解答题
 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为 ,
,查看答案和解析>>
科目: 来源:湖北省高考真题 题型:解答题
查看答案和解析>>
科目: 来源:辽宁省高考真题 题型:单选题
[ ]
查看答案和解析>>
科目: 来源:天津高考真题 题型:解答题
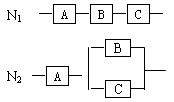
查看答案和解析>>
科目: 来源:天津高考真题 题型:解答题
查看答案和解析>>
科目: 来源:福建省高考真题 题型:填空题
查看答案和解析>>
科目: 来源:广东省高考真题 题型:单选题
查看答案和解析>>
科目: 来源:专项题 题型:解答题
 ,甲、乙、丙三位同学每人购买了一瓶该饮料。
,甲、乙、丙三位同学每人购买了一瓶该饮料。查看答案和解析>>
科目: 来源:陕西省模拟题 题型:解答题
| 某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。 (1)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人; (2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2,表1。 | ||||||||||||
|
表一 | ||||||||||||
表二 | ||||||||||||
| ||||||||||||
  | ||||||||||||
| (ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表)。 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com