【题目】某城市随机抽取一年（365天）内100天的空气质量指数的监测数据，结果统计如下：

记某企业每天由空气污染造成的经济损失（单位：元），空气质量指数为.当时，企业没有造成经济损失；当对企业造成经济损失成直线模型（当时造成的经济损失为，当时，造成的经济损失；当时造成的经济损失为2000元；

（1）试写出的表达式：

（2）在本年内随机抽取一天，试估计该天经济损失超过350元的概率；

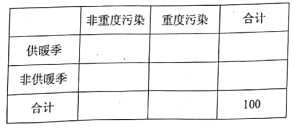
（3）若本次抽取的样本数据有30天是在供暖季，其中有12天为重度污染，完成下面列联表，并判断能否有的把握认为该市本年空气重度污染与供暖有关？

【题目】将函数的图象向右平移个单位，在向上平移一个单位，得到g（x）的图象．若g（x1）g（x2）＝4，且x1，x2∈[﹣2π，2π]，则x1﹣2x2的最大值为（　　）

A. B. C. D.

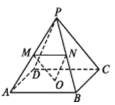
【题目】如图,在棱长均相等的四棱锥中, 为底面正方形的中心, ,分别为侧棱,的中点,有下列结论正确的有：( )

A.∥平面B.平面∥平面

C.直线与直线所成角的大小为D.

【题目】已知函数，．

（1）若在区间上不单调，求的取值范围；

（2）设，若函数在区间恒有意义，求实数的取值范围；

（3）已知方程在有两个不相等的实数根，求实数的取值范围．

【题目】如图，已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB，且ABBP2，AD=AE=1，AE⊥AB，且AE∥BP．

（1）求平面PCD与平面ABPE所成的二面角的余弦值；

（2）线段PD上是否存在一点N，使得直线BN与平面PCD所成角的正弦值等于？若存在，试确定点N的位置；若不存在，请说明理由．

【题目】某同学用“五点法”画函数在某一周期内的图象时，列表并填入了部分数据，如下表：

（1）请将上面表格中①的数据填写在答题卡相应位置上，并直接写出函数的解析式；

（2）若将函数的图象上所有点的横坐标变为原来的倍，纵坐标不变，得到函数的图象，求当时，函数的单调递增区间；

（3）若将函数图象上的所有点向右平移个单位长度，得到的图象. 若图象的一个对称中心为，求的最小值.

【题目】如图所示，在四个正方体中，是正方体的一条体对角线，点分别为其所在棱的中点，能得出平面的图形为（ ）

A.B.

C.D.

【题目】已知两个定点，动点满足.设动点的轨迹为曲线，直线.

（1）求曲线的轨迹方程；

（2）若与曲线交于不同的两点，且（为坐标原点），求直线的斜率；

（3）若， 是直线上的动点，过作曲线的两条切线，切点为，探究：直线是否过定点.

【题目】已知f（x）＝ax+ka﹣x（a＞0且a≠1）是R上的奇函数，且f（1）．

（1）求f（x）的解析式；

（2）若关于x的方程f（1）+f（1﹣3mx﹣2）＝0在区间[0，1]内只有一个解，求m取值集合；

（3）是否存在正整数n，使不得式f（2x）≥（n﹣1）f（x）对一切x∈[﹣1，1]均成立？若存在，求出所有n的值若不存在，说明理由

【题目】在中，内角，，的对边分别是，，，且满足：.

（Ⅰ）求角的大小；

（Ⅱ）若，求的最大值.