
科目: 来源: 题型:
【题目】某校从参加某次知识竞赛的1000同学中,随机抽取60名同学将其成绩(百分制,均为整数)分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)补全频率分布直方图,并估计本次知识竞赛的均分;

(2)如果确定不低于85分的同学进入复赛,问这1000名参赛同学中估计有多少人进人复赛;
(3)若从第一组,第二组和第六组三组学生中分层抽取6人,再从这6人中随机抽取2人,求所抽取的2人成绩之差的绝对值大于20的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某旅游区每年各个月份接待游客的人数近似地满足周期性规律,因而第![]() 个月从事旅游服务工作的人数
个月从事旅游服务工作的人数![]() 可近似地用函数
可近似地用函数![]() 来刻画,其中正整数
来刻画,其中正整数![]() 表示月份且
表示月份且![]() ,例如
,例如![]() 表示1月份,
表示1月份,![]() 和
和![]() 是正整数,
是正整数,![]() ,
,![]() . 统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
. 统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
① 每年相同的月份,该地区从事旅游服务工作的人数基本相同;
② 该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差400人;
③ 2月份该地区从事旅游服务工作的人数为100人,随后逐月递增直到8月份达到最多.
(1)试根据已知信息,求![]() 的表达式;
的表达式;
(2)一般地,当该地区从事旅游服务工作的人数在400或400以上时,该地区也进入了一年中的旅游“旺季”,那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ).当点
).当点![]() 在函数
在函数![]() 图象上运动时,对应的点
图象上运动时,对应的点![]() 在函数
在函数![]() 图象上运动,则称函数
图象上运动,则称函数![]() 是函数
是函数![]() 的相关函数.
的相关函数.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)对任意的![]() ,
,![]() 的图象总在其相关函数图象的下方,求
的图象总在其相关函数图象的下方,求![]() 的取值范围;
的取值范围;
(3)设函数![]() ,
,![]() .当
.当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点![]() 、
、![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,双曲线
的左、右焦点,双曲线![]() 的离心率为
的离心率为![]() ,点
,点![]() 在双曲线
在双曲线![]() 上,不在
上,不在![]() 轴上的动点
轴上的动点![]() 与动点
与动点![]() 关于原点
关于原点![]() 对称,且四边形
对称,且四边形![]() 的周长为
的周长为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线交
的直线交![]() 的轨迹
的轨迹![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 上一点,且满足
上一点,且满足![]() ,其中
,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】材料一:2018年,全国逾半省份将从秋季入学的高一年级开始实行新的学业水平考试和高考制度.所有省级行政区域均突破文理界限,由学生跨文理选科,均设 置“![]() ”的考试科目.前一个“3”为必考科目,为统一高考科目语文、数学、外语.除个别省级行政区域仍执行教育部委托的分省命题任务外,绝大部分省级行政区域均由教育部考试中心统一命题;后一个“3”为高中学业水平考试(简称“学考”)选考科目,由各省级行政区域自主命题.材料二:2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,方案决定从2018年秋季入学的高中一年级学生开始实施高考综合改革.考生总成绩由全国统一高考的语文、数学、外语3个科目成绩和考生选择的3科普通高中学业水平选择性考试科目成绩组成,满分为750分.即通常所说的“
”的考试科目.前一个“3”为必考科目,为统一高考科目语文、数学、外语.除个别省级行政区域仍执行教育部委托的分省命题任务外,绝大部分省级行政区域均由教育部考试中心统一命题;后一个“3”为高中学业水平考试(简称“学考”)选考科目,由各省级行政区域自主命题.材料二:2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,方案决定从2018年秋季入学的高中一年级学生开始实施高考综合改革.考生总成绩由全国统一高考的语文、数学、外语3个科目成绩和考生选择的3科普通高中学业水平选择性考试科目成绩组成,满分为750分.即通常所说的“![]() ”模式,所谓“
”模式,所谓“![]() ”,即“3”是三门主科,分别是语文、数学、外语,这三门科目是必选的.“1”指的是要在物理、历史里选一门,按原始分计入成绩.“2”指考生要在生物、化学、思想政治、地理4门中选择2门.但是这几门科目不以原始分计入成绩,而是等级赋分.等级赋分指的是把考生的原始成绩根据人数的比例分为
”,即“3”是三门主科,分别是语文、数学、外语,这三门科目是必选的.“1”指的是要在物理、历史里选一门,按原始分计入成绩.“2”指考生要在生物、化学、思想政治、地理4门中选择2门.但是这几门科目不以原始分计入成绩,而是等级赋分.等级赋分指的是把考生的原始成绩根据人数的比例分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级,五个等级分别对应着相应的分数区间,然后再用公式换算,转换得出分数.
五个等级,五个等级分别对应着相应的分数区间,然后再用公式换算,转换得出分数.
(1)若按照“![]() ”模式选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
”模式选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
(2)某教育部门为了调查学生语数外三科成绩与选科之间的关系,现从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,满分450分,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分;
①考生甲得知他的成绩为270分,考试后不久了解到如下情况:“此次测试平均成绩为171分,351分以上共有57人”,问甲能否获得荣誉证书,请说明理由;
②考生丙得知他的实际成绩为430分,而考生乙告诉考生丙:“这次测试平均成绩为201分,351分以上共有57人”,请结合统计学知识帮助丙同学辨别乙同学 信息的真伪.
附:![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对![]() 表示“甲在
表示“甲在![]() 号车站下车,乙在
号车站下车,乙在![]() 号车站下车”
号车站下车”
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中点,
的中点,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影为点
上的正投影为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
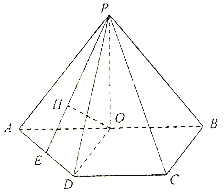
(1)求证:![]() 为
为![]() 中点;
中点;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某年级组织学生参加了某项学术能力测试,为了解参加测试学生的成绩情况,从中随机抽取20名学生的测试成绩作为样本,规定成绩大于或等于80分的为优秀,否则为不优秀.统计结果如图:
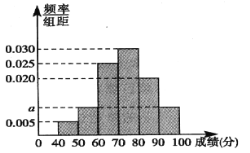
(1)求![]() 的值和样本的平均数;
的值和样本的平均数;
(2)从该样本成绩优秀的学生中任选两名,求这两名学生的成绩至少有一个落在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com